Cho biết \(\cos x = - \frac{{12}}{{13}}\) và \(\pi < x < \frac{{3\pi }}{2}\); khi đó:
a) \(\sin x > 0\)
b) \(\sin x = - \frac{5}{{13}}\)
c) \(\cot x = \frac{5}{{12}}\)
d) \(\sin \left( {\frac{\pi }{3} - x} \right) = \frac{{5 - 12\sqrt 3 }}{{26}}\)
Cho biết \(\cos x = - \frac{{12}}{{13}}\) và \(\pi < x < \frac{{3\pi }}{2}\); khi đó:
a) \(\sin x > 0\)
b) \(\sin x = - \frac{5}{{13}}\)
c) \(\cot x = \frac{5}{{12}}\)
d) \(\sin \left( {\frac{\pi }{3} - x} \right) = \frac{{5 - 12\sqrt 3 }}{{26}}\)
Câu hỏi trong đề: Đề kiểm tra Công thức lượng giác (có lời giải) !!
Quảng cáo
Trả lời:
|
a) Sai |
b) Đúng |
c) Sai |
d) Đúng |
Vì \(\pi < x < \frac{{3\pi }}{2}\) nên \(\sin x < 0\).
Ta có: \(\cos x = - \frac{{12}}{{13}} \Rightarrow \sin x = - \sqrt {1 - {{\cos }^2}x} = - \sqrt {1 - {{\left( { - \frac{{12}}{{13}}} \right)}^2}} = - \frac{5}{{13}}\).
\(\sin \left( {\frac{\pi }{3} - x} \right) = \sin \frac{\pi }{3}\cos x - \cos \frac{\pi }{3}\sin x = \frac{{\sqrt 3 }}{2}\left( { - \frac{{12}}{{13}}} \right) - \frac{1}{2}\left( { - \frac{5}{{13}}} \right) = \frac{{5 - 12\sqrt 3 }}{{26}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
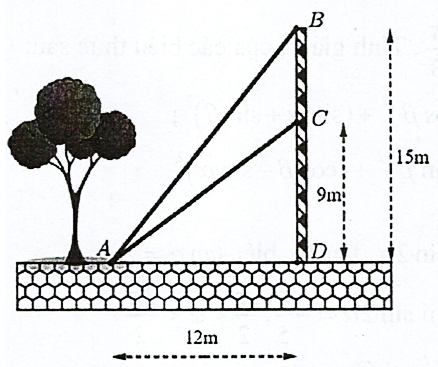
Ta có:
\(\begin{array}{l}\tan \alpha = \tan (\widehat {BAD} - \widehat {CAD})\\ = \frac{{\tan \widehat {BAD} - \tan \widehat {CAD}}}{{1 + \tan \widehat {BAD}\tan \widehat {CAD}}} = \frac{{\frac{{15}}{{12}} - \frac{9}{{12}}}}{{1 + \frac{{15}}{{12}} \cdot \frac{9}{{12}}}} = \frac{8}{{31}}.\end{array}\)
Vì vậy
\(\begin{array}{*{20}{l}}B&{ = \frac{{\sin 2x + 2\sin 3x + \sin 4x}}{{\cos 3x + 2\cos 4x + \cos 5x}} = \frac{{2\sin 3x\cos x + 2\sin 3x}}{{2\cos 4x\cos x + 2\cos 4x}} = \frac{{2\sin 3x(\cos x + 1)}}{{2\cos 4x(\cos x + 1)}} = \frac{{\sin 3x}}{{\cos 4x}}}\\{}&{}\end{array}\)
Câu 2
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biết \(\sin x = \frac{1}{{\sqrt 3 }}\) và \(0 < x < \frac{\pi }{2}\); khi đó:
a) \(\cos x > 0\)
b) \(\cos x = \frac{{\sqrt 6 }}{3}\)
c) \(\tan x = \frac{{\sqrt 3 }}{3}\)
d) \(\cos \left( {x + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 - 3}}{8}{\rm{. }}\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biết \(\sin x = \frac{1}{{\sqrt 3 }}\) và \(0 < x < \frac{\pi }{2}\); khi đó:
a) \(\cos x > 0\)
b) \(\cos x = \frac{{\sqrt 6 }}{3}\)
c) \(\tan x = \frac{{\sqrt 3 }}{3}\)
d) \(\cos \left( {x + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 - 3}}{8}{\rm{. }}\)
Lời giải
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |
a) Vì \(0 < x < \frac{\pi }{2}\) nên \(\cos x > 0\).
Ta có: \(\sin x = \frac{1}{{\sqrt 3 }} \Rightarrow \cos x = \sqrt {1 - {{\sin }^2}x} = \sqrt {1 - \frac{1}{3}} = \frac{{\sqrt 6 }}{3}\).
\(\cos \left( {x + \frac{\pi }{3}} \right) = \cos x\cos \frac{\pi }{3} - \sin x\sin \frac{\pi }{3} = \frac{{\sqrt 6 }}{3} \cdot \frac{1}{2} - \frac{1}{{\sqrt 3 }} \cdot \frac{{\sqrt 3 }}{2} = \frac{{\sqrt 6 - 3}}{6}{\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.