Cho tam giác nhọn \[ABC\] nội tiếp trong đường tròn tâm \[O\] có \[AB < AC\]. Trên cung nhỏ lấy điểm \[M\] khác \[A\] thỏa mãn \[MA < MC\]. Vẽ đường kính \[MN\] của đường tròn \[\left( O \right)\] và gọi \[H,\,K\] lần lượt là hình chiếu vuông góc của \[A\] trên \[MB,\,MN\].
Chứng minh rằng:
a) Bốn điểm \[A,\,H,\,K,\,M\] cùng nằm trên một đường tròn.
b) \[AH.AK = HB.MK\].
c) Khi điểm \[M\] di động trên cung nhỏ thì đường thẳng \[HK\] luôn đi qua một điểm cố định.
Cho tam giác nhọn \[ABC\] nội tiếp trong đường tròn tâm \[O\] có \[AB < AC\]. Trên cung nhỏ lấy điểm \[M\] khác \[A\] thỏa mãn \[MA < MC\]. Vẽ đường kính \[MN\] của đường tròn \[\left( O \right)\] và gọi \[H,\,K\] lần lượt là hình chiếu vuông góc của \[A\] trên \[MB,\,MN\].
Chứng minh rằng:
a) Bốn điểm \[A,\,H,\,K,\,M\] cùng nằm trên một đường tròn.
b) \[AH.AK = HB.MK\].
c) Khi điểm \[M\] di động trên cung nhỏ thì đường thẳng \[HK\] luôn đi qua một điểm cố định.
Quảng cáo
Trả lời:
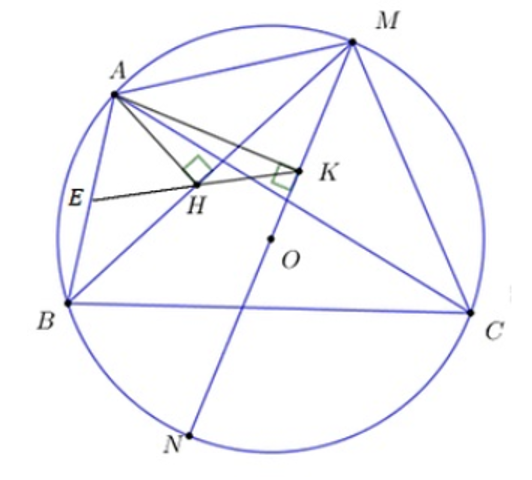
a) Xét tứ giác \[AHKM\] ta có: \[\widehat {AHM} = \widehat {AKM} = 90^\circ \] (gt).
Mà hai góc này là góc kề cạnh \[HK\] và cùng nhìn đoạn \[AM\].
Do đó, \[AHKM\] là tứ giác nội tiếp (dấu hiệu nhận biết).
Hay bốn điểm \[A,\,H,\,K,\,M\] cùng nằm trên một đường tròn (đpcm).
b) Ta có:
Mà .
Mà \[\widehat {ABH} + \widehat {BAH} = 90^\circ \] (tam giác \[ABH\] vuông tại \[H\])
\[ \Rightarrow \widehat {AMK} = \widehat {BAH}\]
Xét tam giác \[AMK\] và tam giác \[BAH\] có:
\[\widehat {AKM} = \widehat {BHA} = 90^\circ \]
\[\widehat {AMK} = \widehat {BAH}\] (cmt)
Do đó, (g.g).
\[ \Rightarrow \frac{{AK}}{{HB}} = \frac{{MK}}{{AH}} \Rightarrow AH.AK = HB.MK\].
c) Kéo dài \[HK\] cắt \[AB\] tại \[E\].
Ta có \[\widehat {MAK} = \widehat {MHK}\] (hai góc nội tiếp cùng chắn cung \[MK\]).
Lại có \[\widehat {MHK} = \widehat {EHB}\] (đối đỉnh)
\[ \Rightarrow \widehat {MAK} = \widehat {EHB}\].
Do (cmt) \[ \Rightarrow \widehat {MAK} = \widehat {ABH} = \widehat {EBH}\].
\[ \Rightarrow \widehat {EHB} = \widehat {EBH}\] \[ \Rightarrow \Delta EHB\] cân tại \[E\].
\[ \Rightarrow EH = EB\] (1).
Ta có \[\widehat {EBH} + \widehat {EAH} = 90^\circ \] (Tam giác \[ABH\] vuông tại \[H\]).
Mà \[\widehat {EHB} + \widehat {EHA} = \widehat {AHB} = 90^\circ \].
Do đó, \[\widehat {EAH} = \widehat {EHA}\] \[ \Rightarrow \Delta EHA\] cân tại \[E\].
\[ \Rightarrow EA = EH\] (2).
Từ (1) và (2) \[ \Rightarrow EA = EB\] \[ \Rightarrow E\] là trung điểm của \[AB\].
Do \[A,\,\,B\] cố định nên \[E\] cố định.
Vậy khi \[M\] di chuyển trên cung nhỏ \[AC\] thì \[HK\] luôn đi qua trung điểm của \[AB\] (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương trình đã cho có hai nghiệm phân biệt \[{x_1},\,{x_2} \Leftrightarrow \Delta ' > 0\]
\[ \Leftrightarrow {\left( {m - 1} \right)^2} - \left( {4m - 11} \right) > 0\]
\[ \Leftrightarrow {m^2} - 2m + 1 - 4m + 11 > 0\]
\[ \Leftrightarrow {m^2} - 6m + 12 > 0\]
\[ \Leftrightarrow {m^2} - 6m + 9 + 3 > 0\]
\[ \Leftrightarrow {\left( {m - 3} \right)^2} + 3 > 0\]
Vì \[{\left( {m - 3} \right)^2} \ge 0\,\,\forall m\] nên \[{\left( {m - 3} \right)^2} + 3 > 0\,\,\forall m \Rightarrow \Delta ' > 0\,\,\forall m\].
Hay phương trình đã cho luôn có hai nghiệm phân biệt \[{x_1},\,{x_2}\] với mọi \[m\].
Áp dụng hệ thức Vi – ét ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\left( {m - 1} \right)\\{x_1}{x_2} = 4m - 11\end{array} \right.\].
Vì \[{x_1},\,{x_2}\] là nghiệm của phương trình \[{x^2} + 2\left( {m - 1} \right)x + 4m - 11 = 0\] nên ta có:
\[\left\{ \begin{array}{l}x_1^2 + 2\left( {m - 1} \right){x_1} + 4m - 11 = 0\\x_2^2 + 2\left( {m - 1} \right){x_2} + 4m - 11 = 0\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}2x_1^2 + 4\left( {m - 1} \right){x_1} + 8m - 22 = 0\\x_2^2 + 2\left( {m - 1} \right){x_2} + 4m - 11 = 0\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}2x_1^2 = - 4\left( {m - 1} \right){x_1} - 8m + 22\\x_2^2 = - 2\left( {m - 1} \right){x_2} - 4m + 11\end{array} \right.\].
Ta có: \[2{\left( {{x_1} - 1} \right)^2} + \left( {6 - {x_2}} \right)\left( {{x_1}{x_2} + 11} \right) = 72\]
\[ \Leftrightarrow 2x_1^2 - 4{x_1} + 2 + 6{x_1}{x_2} + 66 - {x_1}x_2^2 - 11{x_2} = 72\]
\[ \Leftrightarrow - 4\left( {m - 1} \right){x_1} - 8m + 22 - 4{x_1} + 6{x_1}{x_2} - {x_1}\left[ { - 2\left( {m - 1} \right){x_2} - 4m + 11} \right] - 11{x_2} = 4\]
\[ \Leftrightarrow - 4m{x_1} + 4{x_1} - 8m - 4{x_1} + 6{x_1}{x_2} + 2\left( {m - 1} \right){x_1}{x_2} + 4m{x_1} - 11{x_1} - 11{x_2} = - 18\]
\[ \Leftrightarrow \left( {2m + 4} \right){x_1}{x_2} - 11\left( {{x_1} + {x_2}} \right) = 8m - 18\]
\[ \Leftrightarrow \left( {2m + 4} \right)\left( {4m - 11} \right) - 11.\left[ { - 2\left( {m - 1} \right)} \right] = 8m - 18\]
\[ \Leftrightarrow 8{m^2} - 22m + 16m - 44 + 22m - 22 = 8m - 18\]
\[ \Leftrightarrow 8{m^2} + 8m - 48 = 0\]
\[ \Leftrightarrow {m^2} + m - 6 = 0\]
\[ \Leftrightarrow {m^2} - 2m + 3m - 6 = 0\]
\[ \Leftrightarrow m\left( {m - 2} \right) + 3\left( {m - 2} \right) = 0\]
\[ \Leftrightarrow \left( {m - 2} \right)\left( {m + 3} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right.\].
Vậy \[m = - 3\] hoặc \[m = 2\] thì thỏa mãn yêu cầu bài toán.
Lời giải
Gọi độ dài một cạnh góc vuông lớn hơn của tam giác vuông là \[x\] (cm), \[\left( {7 < x < 17} \right)\].
Khi đó độ dài cạnh góc vuông còn lại của tam giác vuông đó là: \[x - 7\] (cm).
Áp dụng định lí Pi-ta-go cho tam giác vuông này ta có phương trình:
\[{x^2} + {\left( {x - 7} \right)^2} = {17^2}\]
\[ \Leftrightarrow 2{x^2} - 14x + 49 = 289\]
\[ \Leftrightarrow 2{x^2} - 14x - 240 = 0\]
\[ \Leftrightarrow 2\left( {x - 15} \right)\left( {x + 8} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}x - 15 = 0\\x + 8 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 15\,\,\,\left( {{\rm{tm}}} \right)\\x = - 8\,\,\,\left( {{\rm{loai}}} \right)\end{array} \right.\]
Suy ra độ dài cạnh còn lại của tam giác vuông là: 15 – 7 = 8 cm.
Vậy diện tích của tam giác vuông đó là: \[S = \frac{1}{2}.8.15 = 60\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.