Cho tam giác nhọn \(ABC\) có \(AB < AC,\) các đường cao \(BD,CE\) \(\left( {D \in AC,E \in AB} \right)\) cắt nhau tại \(H.\)
a) Chứng minh rằng tứ giác \(BEDC\) nội tiếp.
b) Gọi \(M\) là trung điểm của \(BC.\) Đường tròn đường kính \(AH\) cắt \(AM\) tại điểm \(G\) (\(G\) khác \(A\)). Chứng minh rằng \(AE.AB = AG.AM\).
c) Hai đường thẳng \(DE\) và \(BC\) cắt nhau tại \(K.\) Chứng minh rằng \(\widehat {MAC} = \widehat {GCM}\) và đường thẳng nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MC{\rm{D}}\)song song với đường thẳng \(KG.\)
Cho tam giác nhọn \(ABC\) có \(AB < AC,\) các đường cao \(BD,CE\) \(\left( {D \in AC,E \in AB} \right)\) cắt nhau tại \(H.\)
a) Chứng minh rằng tứ giác \(BEDC\) nội tiếp.
b) Gọi \(M\) là trung điểm của \(BC.\) Đường tròn đường kính \(AH\) cắt \(AM\) tại điểm \(G\) (\(G\) khác \(A\)). Chứng minh rằng \(AE.AB = AG.AM\).
c) Hai đường thẳng \(DE\) và \(BC\) cắt nhau tại \(K.\) Chứng minh rằng \(\widehat {MAC} = \widehat {GCM}\) và đường thẳng nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MC{\rm{D}}\)song song với đường thẳng \(KG.\)
Quảng cáo
Trả lời:
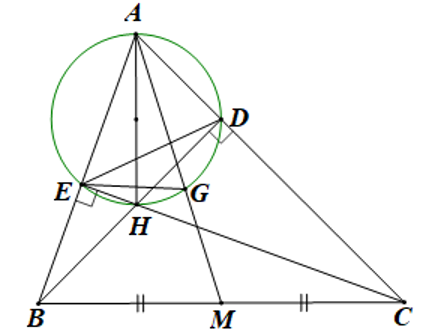
a) Chứng minh rằng tứ giác \(BEDC\) nội tiếp.
Xét tứ giác \(BEDC\) có:
\(\widehat {BDC} = 90^\circ \) (\[BD\] là đường cao)
\(\widehat {BEC} = 90^\circ \) (\[CE\] là đường cao)
\( \Rightarrow \widehat {BDC} = \widehat {BEC} = 90^\circ \), mà hai góc này kề nhau cùng nhìn đoạn \(BC\) một góc bằng \(90^\circ \).
\( \Rightarrow BEDC\) là tứ giác nội tiếp.
b) Gọi \(M\) là trung điểm của \(BC.\) Đường tròn đường kính \(AH\) cắt \(AM\) tại điểm \(G\) (\(G\) khác \(A\)). Chứng minh rằng \(AE.AB = AG.AM\).
Xét tứ giác \(AEHD\) có:
\(\widehat {AEH} = \widehat {ADH} = 90^\circ \)(gt)
\( \Rightarrow \widehat {AEH} + \widehat {ADH} = 90^\circ + 90^\circ = 180^\circ \), mà hai góc này ở vị trí đối nhau.
\( \Rightarrow AEHD\) là tứ giác nội tiếp đường tròn đường kính \(AH\).
\( \Rightarrow \widehat {AGE} = \widehat {ADE}\) (góc nội tiếp cùng chắn ) \(\left( 1 \right)\)
Ta có: tứ giác \(BEDC\) nội tiếp (theo câu a)
\( \Rightarrow \widehat {EBC} = \widehat {ADE}\) (góc ngoài của tứ giác nội tiếp) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\),\(\left( 2 \right)\)\( \Rightarrow \widehat {AGE} = \widehat {EBC}\) hay \(\widehat {AGE} = \widehat {ABM}\)
Xét \(\Delta AGE\) và \(\Delta ABM\)có:
\(\widehat A\) là góc chung;
\(\widehat {AGE} = \widehat {ABM}\) (chứng minh trên).
\( \Rightarrow \frac{{AG}}{{AB}} = \frac{{AE}}{{AM}}\) (tỉ số đồng dạng)
\( \Rightarrow AE.AB = AG.AM\) (đpcm)
c) Hai đường thẳng \(DE\) và \(BC\) cắt nhau tại \(K.\) Chứng minh rằng \(\widehat {MAC} = \widehat {GCM}\) và đường thẳng nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MC{\rm{D}}\)song song với đường thẳng \(KG.\)
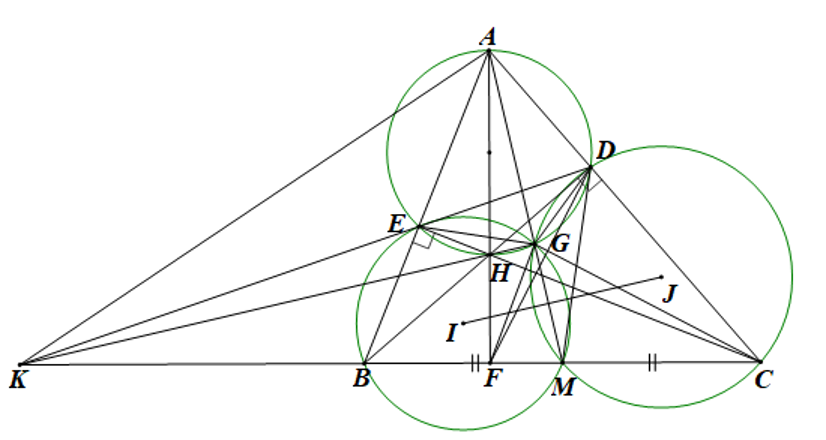
• Xét đường tròn đường kính \(AH\) có: \(\widehat {AGD} = \widehat {AED}\) (góc nội tiếp cùng chắn )
Mà \(\widehat {AED} = \widehat {DCB}\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác \(BEDC\) nội tiếp)
\( \Rightarrow \widehat {AGD} = \widehat {ACB} = \widehat {DCM}\)
Lại có: \(\widehat {AGD} + \widehat {DGM} = 180^\circ \) (kề bù)
\( \Rightarrow \widehat {DGM} + \widehat {DCM} = 180^\circ \), mà hai góc này ở vị trí đối nhau
\( \Rightarrow GDCM\) là tứ giác nội tiếp.
\( \Rightarrow \widehat {MGC} = \widehat {MDC}\) (hai góc nội tiếp cùng chắn cung \(MC\)) \(\left( 1 \right)\)
Lại có: \(DM = \frac{1}{2}BC = MC\) (định lí đường trung tuyến trong tam giác vuông)
\( \Rightarrow \Delta MCD\) cân tại \(M\).
\( \Rightarrow \widehat {MDC} = \widehat {MCD}\) (hai góc ở đáy của tam giác cân) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\),\(\left( 2 \right)\)\( \Rightarrow \widehat {MGC} = \widehat {MCD}\) hay \( \Rightarrow \widehat {MGC} = \widehat {MCA}\)
Xét \(\Delta GCM\) và \(\Delta CAM\)có:
\(\widehat {AMC}\) là góc chung;
\(\widehat {MGC} = \widehat {MCA}\) (chứng minh trên)
\( \Rightarrow \widehat {GCM} = \widehat {CAM}\) (hai góc tương ứng) (điều phải chứng minh).
• Ta có: \(\widehat {AGE} = \widehat {ABM}\) (chứng minh câu b) hay \(\widehat {AGE} = \widehat {EBM}\)
Mà: \(\widehat {AGE} + \widehat {EGM} = 180^\circ \) (kề bù)
\( \Rightarrow \widehat {EBM} + \widehat {EGM} = 180^\circ \), mà hai góc này ở vị trí đối nhau
\( \Rightarrow GEBM\) là tứ giác nội tiếp
Ta có hai tứ giác \(GEBM,GDCM\) là các tứ giác nội tiếp
Þ Đường nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MCD\) là đường nối tâm hai đường tròn ngoại tiếp hai tứ giác \(GEBM,GDCM\).
Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(GEBM\), \(J\) là tâm đường tròn ngoại tiếp tứ giác \(GDCM\)
Mà giao của hai tứ giác \(GEBM,GDCM\) là \(GM\)
\( \Rightarrow IJ \bot GM\) \(\left( * \right)\)
Gọi \(\left\{ F \right\} = AH \cap BC\)\( \Rightarrow AF \bot BC \Rightarrow \widehat {AFB} = 90^\circ \)
Xét tứ giác \(ADFB\) có: \(\widehat {AFB} = \widehat {BDA} = 90^\circ \), mà hai góc này cùng nhìn đoạn \(AB\) dưới 1 góc bằng \(90^\circ \)
\( \Rightarrow ADFB\) là tứ giác nội tiếp.
\( \Rightarrow \widehat {BAC} = \widehat {DFM}\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp) \(\left( 3 \right)\)
Mà \(\widehat {EDH} = \widehat {EAH}\) (hai góc nội tiếp cùng chắn cung \(EH\)) \(\left( 4 \right)\)
Lại có: \(DM = \frac{1}{2}BC = BM\) (định lí đường trung tuyến trong tam giác vuông)
\( \Rightarrow \Delta MBD\) cân tại \(M\).
\( \Rightarrow \widehat {BDM} = \widehat {DBM}\) hay \(\widehat {HDM} = \widehat {DBM}\)
Mà \(\widehat {DBM} = \widehat {HAD}\) (cùng phụ với \(\widehat {ACB}\))
\( \Rightarrow \widehat {HDM} = \widehat {HAD}\) \(\left( 5 \right)\)
Từ \(\left( 3 \right)\),\(\left( 4 \right)\),\(\left( 5 \right)\)\( \Rightarrow \widehat {EDM} = \widehat {EDH} + \widehat {HDM} = \widehat {EAH} + \widehat {HAD} = \widehat {BAC} = \widehat {DFM} = \widehat {KDM}\)
Xét \(\Delta FDM\) và \(\Delta DKM\) có:
\(\widehat {KMD}\) là góc chung;
\(\widehat {DFM} = \widehat {KDM}\) (chứng minh trên)
\( \Rightarrow \frac{{MD}}{{MK}} = \frac{{FM}}{{DM}}\) (tỉ số đồng dạng)
\[ \Rightarrow M{D^2} = FM.MK\]
Có: (chứng minh trên) \( \Rightarrow \frac{{MC}}{{MA}} = \frac{{GM}}{{CM}} \Rightarrow M{C^2} = GM.MA\)
Mà \(MD = MC\) (chứng minh trên)
\( \Rightarrow FM.MK = GM.MA \Rightarrow \frac{{FM}}{{GM}} = \frac{{MA}}{{MK}}\)
\( \Rightarrow \widehat {FGM} = \widehat {AKM}\) (hai góc ương ứng)
\( \Rightarrow AGFK\) là tứ giác nội tiếp (tứ giác có goc ngoài bằng góc trong của đỉnh đối diện).
\( \Rightarrow \widehat {AGK} = \widehat {AFK} = 90^\circ \) (hai góc nội tiếp cùng chắn cung \(AK\))
\( \Rightarrow KG \bot AG\) hay \(KG \bot GM\) \(\left( {**} \right)\)
Từ \(\left( * \right)\),\(\left( {**} \right)\)\( \Rightarrow IJ{\rm{ // }}KG\)
Vậy đường tròn nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MCD\) song song với \(KG\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Với \(m = 2\) thì phương trình \(\left( * \right)\) trở thành:
\({x^2} + 4x - 12 = 0\)
\( \Leftrightarrow {x^2} + 6x - 2x - 12 = 0\)
\( \Leftrightarrow x\left( {x + 6} \right) - 2\left( {x + 6} \right) = 0\)
\( \Leftrightarrow \left( {x + 6} \right)\left( {x - 2} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 6 = 0}\\{x - 2 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 6}\\{x = 2}\end{array}} \right.\)
Vậy với \(m = 2\) thì phương trình \(\left( * \right)\) có tập nghiệm là \(S = \left\{ { - 6;2} \right\}\).
b) Phương trình \(\left( * \right)\) có \(a.c = 1.\left( { - 12} \right) = - 12 < 0\) nên luôn có hai nghiệm phân biệt trái dấu \({x_1},{x_2}\).
Theo định lí Vi-et ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - 4m + 4}\\{{x_1}.{x_2} = - 12}\end{array}} \right.\) \(\left( 1 \right)\)
Vì \({x_2}\) là nghiệm của phương trình \(\left( * \right)\) nên ta có: \(x_2^2 + 4\left( {m - 1} \right){x_2} - 12 = 0\)
\( \Leftrightarrow x_2^2 + 4m{x_2} - 4{x_2} - 12 = 0\)
\( \Leftrightarrow x_2^2 + 4\left( {m{x_2} - 4} \right) - 4{x_2} + 4 = 0\)
\( \Leftrightarrow 4\left( {4 - m{x_2}} \right) = x_2^2 - 4{x_2} + 4\)
\( \Leftrightarrow 4\left( {4 - m{x_2}} \right) = {\left( {{x_2} - 2} \right)^2}\)
\( \Leftrightarrow 2.\sqrt {4 - m{x_2}} = \sqrt {{{\left( {{x_2} - 2} \right)}^2}} \)
\( \Leftrightarrow 2.\sqrt {4 - m{x_2}} = \left| {{x_2} - 2} \right|\) \(\left( 2 \right)\)
Mà theo bài có: \(4\left| {{x_1} - 2} \right|.\sqrt {4 - m{{\rm{x}}_2}} = {\left( {{x_1} + {x_2} - {x_1}{x_2} - 8} \right)^2}\) \(\left( 3 \right)\)
Thay \(\left( 1 \right)\),\(\left( 2 \right)\) vào \(\left( 3 \right)\) ta được: \(2.\left| {{x_1} - 2} \right|.\left| {{x_2} - 2} \right| = {\left( { - 4m + 4 + 12 - 8} \right)^2}\)
\( \Leftrightarrow 2.\left| {\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right)} \right| = {\left( {8 - 4m} \right)^2}\)
\( \Leftrightarrow 2.\left| {{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4} \right| = {4^2}.{\left( {2 - m} \right)^2}\)
\( \Leftrightarrow 2.\left| { - 12 - 2\left( { - 4m + 4} \right) + 4} \right| = 16{\left( {m - 2} \right)^2}\)
\( \Leftrightarrow 2.\left| { - 16 + 8m} \right| = 16{\left( {m - 2} \right)^2}\)
\( \Leftrightarrow 16.\left| {m - 2} \right| = 16{\left( {m - 2} \right)^2}\)
\( \Leftrightarrow \left| {m - 2} \right| = {\left( {m - 2} \right)^2}\)
\( \Leftrightarrow {\left( {m - 2} \right)^2} = {\left( {m - 2} \right)^4}\)
\( \Leftrightarrow {\left( {m - 2} \right)^4} - {\left( {m - 2} \right)^2} = 0\)
\( \Leftrightarrow {\left( {m - 2} \right)^2}.\left[ {{{\left( {m - 2} \right)}^2} - 1} \right] = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\left( {m - 2} \right)}^2} = 0}\\{{{\left( {m - 2} \right)}^2} - 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - 2 = 0}\\{{{\left( {m - 2} \right)}^2} = 1}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - 2 = 0}\\{m - 2 = 1}\\{m - 2 = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2}\\{m = 3}\\{m = 1}\end{array}} \right.\)
Vậy \(m \in \left\{ {1;2;3} \right\}\).
rrow {x^2} + 1000x - 750000 = 0\)
\( \Leftrightarrow {x^2} + 1500x - 500x - 750000 = 0\)
\( \Leftrightarrow x\left( {x + 1500} \right) - 500\left( {x + 1500} \right) = 0\)
\( \Leftrightarrow \left( {x + 1500} \right)\left( {x - 500} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 1500 = 0}\\{x - 500 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1500\left( {ktm} \right)}\\{x = 500\left( {tm} \right)}\end{array}} \right.\)
Vậy theo kế hoạch, địa phương này cần \(\frac{{12000}}{{500}} = 24\) (giờ) để xét nghiệm xong.
Lời giải
Với \(x > 0;x \ne 4\) ta có:
\(B = \left( {\frac{{\sqrt x }}{{2 + \sqrt x }} + \frac{{x + 4}}{{4 - x}}} \right):\frac{x}{{x - 2\sqrt x }}\)
\(B = \left[ {\frac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x + 2} \right).\left( {\sqrt x - 2} \right)}} - \frac{{x + 4}}{{\left( {\sqrt x + 2} \right).\left( {\sqrt x - 2} \right)}}} \right]:\frac{x}{{\sqrt x \left( {\sqrt x - 2} \right)}}\)
\(B = \frac{{x - 2\sqrt x - x - 4}}{{\left( {\sqrt x + 2} \right).\left( {\sqrt x - 2} \right)}} \cdot \frac{{\sqrt x \left( {\sqrt x - 2} \right)}}{x}\)
\(B = \frac{{ - 2\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right).\left( {\sqrt x - 2} \right)}} \cdot \frac{{\sqrt x \left( {\sqrt x - 2} \right)}}{x} = \frac{{ - 2}}{{\sqrt x }}.\)
Vậy với \(x > 0;x \ne 4\) thì \(B = \frac{{ - 2}}{{\sqrt x }}.\)
Xét \(B < - \sqrt x \)\( \Leftrightarrow \frac{{ - 2}}{{\sqrt x }} < - \sqrt x \)\( \Leftrightarrow - 2 < - x \Leftrightarrow x < 2\)
Mà \(x \in \mathbb{Z}\) và \(x > 0;x \ne 4\) nên \(x = 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.