Thu gọn biểu thức \[A = \frac{{2 - \sqrt 3 }}{{1 + \sqrt {4 + 2\sqrt 3 } }} + \frac{{2 + \sqrt 3 }}{{1 - \sqrt {4 - 2\sqrt 3 } }}\].

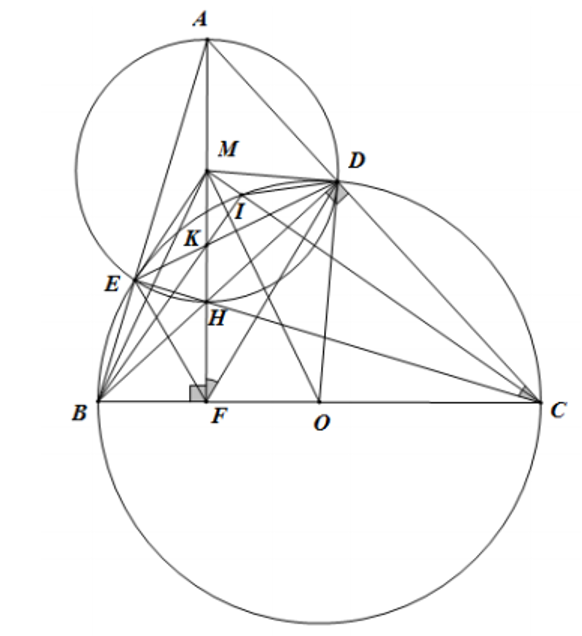
a) Ta có \(\widehat {BEC} = \widehat {BDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Suy ra \(BD \bot AC\) và \(CE \bot AB\). Mà \(BD\) cắt \(CE\) tại \(H\) nên \(H\) là trực tâm \(\Delta ABC\).

Suy ra \[AH \bot BC\]

Vì \[AH \bot BC,\,BD \bot AC\] nên \[\widehat {HFC} = \widehat {HDC} = 90^\circ \]

Suy ra \[\widehat {HFC} + \widehat {HDC} = 180^\circ \]

Suy ra \[HFCD\] là tứ giác nội tiếp

\[ \Rightarrow \widehat {HFD} = \widehat {HCD}\]

b) Vì \[M\] là trung điểm cạnh huyền của tam giác vuông \[ADH\] nên \[MD = MA = MH\]

Tương tự ta có \[ME = MA = MH\]

Suy ra \[MD = ME\]

Mà \[OD = OE\] nên \[\Delta OEM = \Delta ODM\](c.c.c) \[ \Rightarrow \widehat {MOE} = \widehat {MOD} = \frac{1}{2}\widehat {EOD}\] (1)

Theo quan hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có \[\widehat {ECD} = \frac{1}{2}\widehat {EOD}\] (2)

Theo ý a) ta có \[\widehat {HFD} = \widehat {HCD} = \widehat {ECD}\] (3)

Từ (1), (2), (3) suy ra \[\widehat {MOD} = \widehat {HFD}\] hay \[\widehat {MOD} = \widehat {MFD}\]

Suy ra tứ giác \[MFOD\] là tứ giác nội tiếp (4)

\[ \Rightarrow \widehat {MDO} = 180^\circ  - \widehat {MFO} = 90^\circ  \Rightarrow MD \bot DO\]

Chứng minh tương tự ta có \[MEFO\] là tứ giác nội tiếp (5)

Từ (4) và (5) suy ra 5 điểm \[M,\,E,\,F,\,O,\,D\] cùng thuộc 1 đường tròn.

c) Gọi \[I\] là giao điểm thứ hai của \[MC\] với đường tròn \[\left( O \right)\]

Ta có \[\widehat {MDE} = \widehat {DCE}\] (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, cùng chắn cung \[DE\]) hay \[\widehat {MDK} = \widehat {HCD}\]

Mà \[\widehat {HCD} = \widehat {HFD}\](cmt) \[ \Rightarrow \widehat {MDK} = \widehat {HFD}\] hay \[\widehat {MDK} = \widehat {MFD}\]

Suy ra tam giác \[MDK\] đồng dạng với tam giác \[MFD\] (g-g)

\[ \Rightarrow \frac{{MD}}{{MF}} = \frac{{MK}}{{MD}} \Rightarrow M{D^2} = MK.MF\]

Ta có \[\widehat {MDI} = \widehat {MCD}\] (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, cùng chắn cung \[DI\])

Suy ra tam giác \[MDI\] đồng dạng với tam giác \[MCD\] (g-g)