Điểm \[A\left( { - 1;\,3} \right)\] là điểm thuộc miền nghiệm của bất phương trình:
Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
+)Thay \[x = - 1;\,y = 3\] vào bất phương trình \[ - 3x + 2y - 4 > 0\] ta được \[ - 3.( - 1) + 2.3 - 4 = 5 > 0\] là một mệnh đề đúng. Do đó A đúng.
+) Thay \[x = - 1;\,y = 3\] vào bất phương trình \[x + 3y < 0\] ta được \[ - 1 + 3.3 = 8 < 0\] là một mệnh đề sai. Do đó B sai.
+) Thay \[x = - 1;\,y = 3\]vào bất phương trình \[3x - y > 0\] ta được \[3.( - 1) - 3 = - 6 > 0\] là một mệnh đề sai. Do đó C sai.
+) Thay \[x = - 1;\,y = 3\]vào bất phương trình \[2x - y + 4 > 0\] ta được \[2.( - 1) - 3 + 4 = - 1 > 0\] là một mệnh đề sai. Do đó D sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Coi người quan sát từ điểm \[A\] cách gốc cây \[B\] một khoảng bằng \[30\]m, nhìn ngọn cây \[C\] dưới góc \[45^\circ \]. Ta có hình vẽ sau:
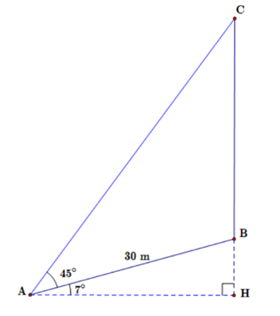
Khi đó \[AB = 30\,\,m,\widehat {CAH} = 45^\circ \].
Do sườn đồi có độ dốc \[12\% \], nên sườn đồi tạo với phương ngang một góc \[\widehat {BAH} \approx 7^\circ \].
Từ đó \[\widehat {BAC} = \widehat {HAC} - \widehat {HAB} \approx 45^\circ - 7^\circ = 38^\circ \] và \[\widehat {BCA} = 45^\circ \].
Áp dụng định lí sin cho tam giác \[ABC\], ta được:
\[BC = \frac{{AB}}{{\sin \widehat {BCA}}}.\sin \widehat {BAC} = \frac{{30}}{{\sin 38^\circ }}.\sin 45^\circ \approx 26\](m).
Vậy chiều cao của cây khoảng \(26\,\,m\).
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
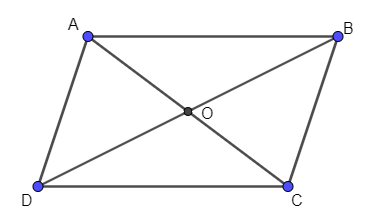
Áp dụng quy tắc hình bình hành ta được:
\[\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \]. Do đó A sai, B đúng.
Ta có: O là tâm của hình bình hành nên \(\overrightarrow {AC} = 2\overrightarrow {AO} \)
Khi đó \[\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} \]. Do đó C đúng.
\[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) = \overrightarrow 0 \]. Do đó D đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.