Cho tam giác \(ABC\) thỏa mãn \({\sin ^2}A = \sin B.\sin C\). Khẳng định nào dưới đây là đúng?

Hướng dẫn giải

Đáp án đúng là: A

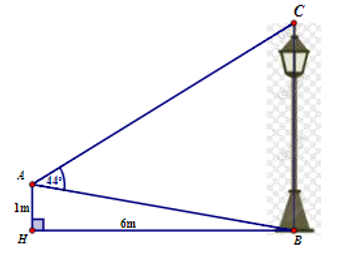
Xét tam giác \(AHB\) vuông tại \(H\), có:

\(A{B^2} = A{H^2} + H{B^2} = {1^2} + {6^2} = 37\)

\( \Leftrightarrow AB = \sqrt {37} \,\,cm\)

\(\tan ABH = \frac{{AH}}{{BH}} = \frac{1}{6} \Rightarrow \widehat {ABH} \approx 9,5^\circ \).

\( \Rightarrow \widehat {ABC} = 90^\circ - 9,5^\circ = 80,5^\circ \)

\( \Rightarrow \widehat {ACB} = 180^\circ - 80,5^\circ - 44^\circ = 55,5^\circ \)

Áp dụng định lí sin trong tam giác \(ABC\), có:

\(\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{BC}}{{\sin \widehat {BAC}}} \Leftrightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{\sqrt {37} .\sin 44^\circ }}{{\sin 55,5^\circ }} \approx 5,1\,\,\left( m \right).\)

Vậy chiều cao của cây đèn đường khoảng \(5,1\,\,m\).

Hướng dẫn giải

Đáp án đúng là: A

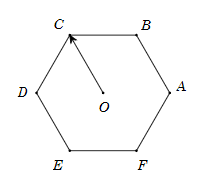
Các vectơ bằng bằng \(\overrightarrow {OC} \) có điểm đầu và điểm cuối là các đỉnh của lục giác là: \(\overrightarrow {BA} ,\,\,\overrightarrow {ED} \).

Vậy có 2 vectơ thỏa mãn điều kiện.