II. Tự luận (4 điểm)

(1 điểm) Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát của hai thành phố Hà Nội và Điện Biên. Khi vệ tinh nằm giữa hai trạm này, góc nâng của nó được quan sát đồng thời là \(40^\circ \) tại Hà Nội và \(85^\circ \) tại Điện Biên. Hỏi vệ tinh đó cách trạm quan sát Điện Biên bao xa? Biết rằng, khoảng cách giữa hai trạm quan sát là 487 km.

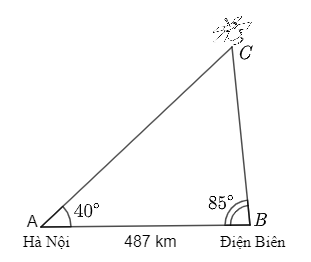
Gọi \(A,\,B,\,\,C\) lần lượt là vị trí trạm quan sát tại Hà Nội, tại Điện Biên và vị trí vệ tinh khi nằm giữa hai trạm trên. Khi đó ta có \(\widehat A = 40^\circ ,\,\widehat B = 85^\circ ,\,AB = 487\) km.

Khoảng cách giữa vệ tinh và trạm quan sát Điện Biên lúc này chính là độ dài \(BC\).

Tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat C = 180^\circ \), suy ra \(\widehat C = 180^\circ  - \left( {\widehat A + \widehat B} \right) = 180^\circ  - \left( {40^\circ  + 85^\circ } \right) = 55^\circ \)

Áp dụng định lí sin trong tam giác \(ABC\) ta có:

\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Rightarrow BC = \frac{{AB\sin A}}{{\sin C}} = \frac{{487 \cdot \sin 40^\circ }}{{\sin 55^\circ }} \approx 382,15\) (km).

Vậy vệ tinh cách trạm quan sát Điện Biên khoảng 382,15 km.