Cho biết \[2\cos \alpha + \sqrt 2 \sin \alpha = 2,\,0^\circ < \alpha < 90^\circ \]. Tính giá trị của \[\cot \alpha \]?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
\[\begin{array}{l}2\cos \alpha + \sqrt 2 \sin \alpha = 2\\ \Leftrightarrow \sqrt 2 \sin \alpha = 2 - 2\cos \alpha \\ \Rightarrow 2{\sin ^2}\alpha = {\left( {2 - 2\cos \alpha } \right)^2}\\ \Leftrightarrow 2 - 2{\cos ^2}\alpha = 4 - 8\cos \alpha + 4{\cos ^2}\alpha \\ \Leftrightarrow 6{\cos ^2}\alpha - 8\cos \alpha + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}\cos \alpha = 1\\\cos \alpha = \frac{1}{3}\end{array} \right.\end{array}\]
Nếu \[\cos \alpha = 1\]: không thỏa mãn vì \[0^\circ < \alpha < 90^\circ \].
Nếu \[\cos \alpha = \frac{1}{3} \Rightarrow \sin \alpha = \frac{{2\sqrt 2 }}{3} \Rightarrow \cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{\sqrt 2 }}{4}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Theo định nghĩa hai vectơ \[\overrightarrow a \] và \[\overrightarrow b \] được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài.
Lời giải
Hướng dẫn giải
Gọi số tiền mà doanh nghiệp A dự định giảm giá là \(x\) ( triệu đồng) \(\left( {0 \le x \le 4} \right)\).
Tiền lãi khi bán được một xe là: \(31 - x - 27 = 4 - x\)(triệu đồng).
Số lượng xe bán được khi đã giảm giá là: \(600 + 200x\) (xe).
Lợi nhuận cửa hàng thu được là: \(\left( {600 + 200x} \right)\left( {4 - x} \right) = - 200{x^2} + 200x + 2\,\,400\)(triệu đồng).
Xét hàm số bậc hai \(y = - 200{x^2} + 200x + 2\,\,400\), có:
Đỉnh \(I\) có tọa độ: \({x_I} = - \frac{b}{{2a}} = - \frac{{200}}{{2.\left( { - 200} \right)}} = \frac{1}{2}\); \({y_I} = - \frac{\Delta }{{4a}} = - \frac{{1\,\,960\,\,000}}{{4.\left( { - 200} \right)}} = 2\,\,450\).
Hay \(I\left( {\frac{1}{2};2\,\,450} \right)\)
Ta có bảng biến thiên:
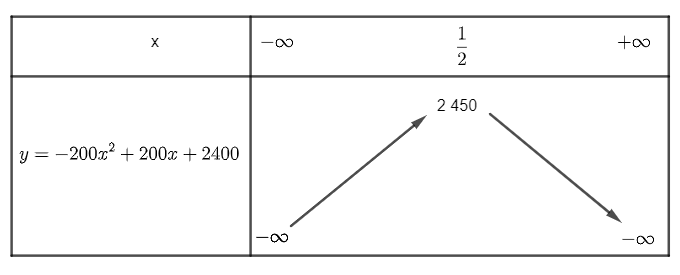
Dựa vào bảng biến thiên ta thấy, hàm số đạt giá trị lớn nhất là \(2\,450\) khi x = \(\frac{1}{2}\).
Vậy doanh nghiệp phải bán với giá \(30,5\) triệu đồng để lợi nhuận thu được là cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Một cửa hàng bán quần áo thời trang đang mở một chương trình khuyến mãi trong vòng 4 ngày, biết rằng số sản phẩm bán được mỗi ngày đều tăng khoảng \[30\% \] so với ngày trước đó. Nhân viên bán hàng đã thống kê số sản phẩm bán được mỗi ngày như bảng dưới đây:
Chọn phát biểu đúng:
|
Ngày |
1 |
2 |
3 |
4 |
|
Số sản phẩm bán được |
50 |
66 |
93 |
115 |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.