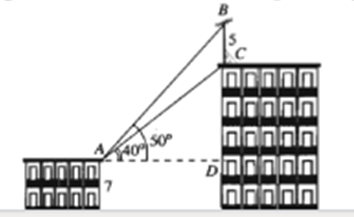
Trên nóc một tòa nhà có một ăng-ten cao \[5m\] . Từ vị trí quan sát \[A\] cao \[7m\] so với mặt đất có thể nhìn thấy đỉnh \[B\] và chân \[C\] của cột ăng-ten dưới góc \[50^\circ \] và \[40^\circ \] so với phương nằm ngang.

Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?

Hướng dẫn giải

Gọi số tiền mà doanh nghiệp A dự định giảm giá là \(x\) ( triệu đồng) \(\left( {0 \le x \le 4} \right)\).

Tiền lãi khi bán được một xe là: \(31 - x - 27 = 4 - x\)(triệu đồng).

Số lượng xe bán được khi đã giảm giá là: \(600 + 200x\) (xe).

Lợi nhuận cửa hàng thu được là: \(\left( {600 + 200x} \right)\left( {4 - x} \right) = - 200{x^2} + 200x + 2\,\,400\)(triệu đồng).

Xét hàm số bậc hai \(y = - 200{x^2} + 200x + 2\,\,400\), có:

Đỉnh \(I\) có tọa độ: \({x_I} = - \frac{b}{{2a}} = - \frac{{200}}{{2.\left( { - 200} \right)}} = \frac{1}{2}\); \({y_I} = - \frac{\Delta }{{4a}} = - \frac{{1\,\,960\,\,000}}{{4.\left( { - 200} \right)}} = 2\,\,450\).

Hay \(I\left( {\frac{1}{2};2\,\,450} \right)\)

Ta có bảng biến thiên:

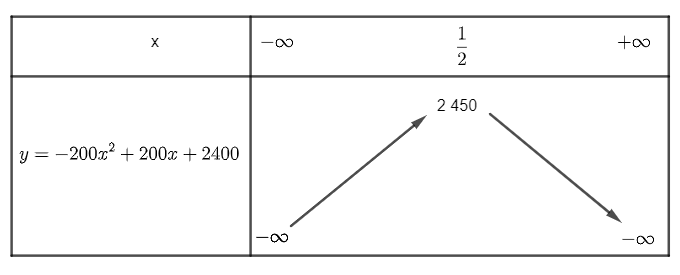
Dựa vào bảng biến thiên ta thấy, hàm số đạt giá trị lớn nhất là \(2\,450\) khi x = \(\frac{1}{2}\).

Vậy doanh nghiệp phải bán với giá \(30,5\) triệu đồng để lợi nhuận thu được là cao nhất.

Hướng dẫn giải

Đáp án đúng là: B

Theo định nghĩa hai vectơ \[\overrightarrow a \] và \[\overrightarrow b \] được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài.