Trong một trường THPT có 8 lớp 10, mỗi lớp cử 2 học sinh đi tham gia buổi họp của đoàn trường. Trong buổi họp ban tổ chức cần chọn ra 4 học sinh từ 16 học sinh của khối 10 để phát biểu ý kiến. Có bao nhiêu cách chọn sao cho trong 4 học sinh được chọn có đúng hai học sinh học cùng một lớp.

Gọi \(x\,\,\left( {0 < x < 10} \right)\) là chiều rộng của khu vườn.

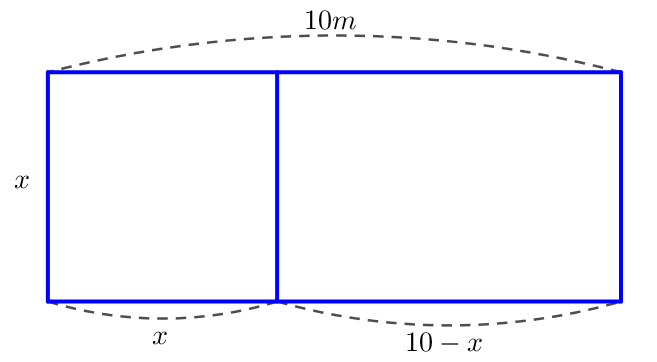
Khi đó : Diện tích phần đất trồng rau là \({x^2}\) \(\left( {{m^2}} \right)\)

Diện tích hồ nuôi cá là \(10x - {x^2}\) \(\left( {{m^2}} \right)\)

Theo giả thiết đề ra ta có bất phương trình: \(60000{x^2} + 135000\left( {10x - {x^2}} \right) \le 5400000\)

\( \Leftrightarrow  - 75000{x^2} + 1350000x - 5400000 \le 0\)\( \Leftrightarrow x \le 6\) (nhận) \( \vee \) \(x \ge 12\) (loại)\( \Rightarrow 0 < x \le 6\)

Vậy chiều rộng khu vườn lớn nhất có thể là \(6m\).

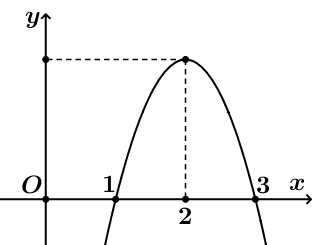
Ta có: \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = m\\x = m + 3\end{array} \right.\).

\(f\left( x \right) < 0 \Leftrightarrow x \in \left( {m;m + 3} \right)\)

Do đó: \(f\left( x \right) < 0,\forall x \in \left( { - 1;0} \right)\) \( \Leftrightarrow \) \(\left( { - 1;0} \right) \subset \left( {m;m + 3} \right)\) \( \Leftrightarrow \) \(m \le  - 1 < 0 \le m + 3\)\( \Leftrightarrow \left\{ \begin{array}{l}m \le  - 1\\0 \le m + 3\end{array} \right.\).\( \Leftrightarrow \left\{ \begin{array}{l}m \le  - 1\\ - 3 \le m\end{array} \right. \Leftrightarrow  - 3 \le m \le  - 1\)

Vậy \( - 3 \le m \le  - 1\)\( \Rightarrow m \in \left\{ { - 3;\, - 2;\, - 1} \right\}\) nên có \(3\) giá trị nguyên thỏa mãn.