Bộ 5 đề thi cuối kì 2 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 4
26 người thi tuần này 4.6 207 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
106 lượt thi
20 câu hỏi
Danh sách câu hỏi:
Câu 1
A. \(f\left( x \right) = 2{x^3} - x + 1\).
B. \(f\left( x \right) = - 2x + 1\).
C. \(f\left( x \right) = 2{x^2} - x + 1\).
D. \(f\left( x \right) = \sqrt {{x^2} - 2x + 3} \).
Lời giải
Tam thức bậc hai là biểu thức có dạng \(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right)\).
Do đó \(f\left( x \right) = 2{x^2} - x + 1\)là tam thức bậc hai.
Câu 2
A. \[2 < x < 3\].
B. \[\left[ \begin{array}{l}x > 2\\x < 1\end{array} \right.\].
C. \[1 < x < 2\].
D. \[\left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\].
Lời giải
Tam thức \(f\left( x \right) = {x^2} - 3x + 2\) có \(\Delta = 1\) nên \(f\left( x \right)\) có hai nghiệm \(x = 1\,;\,\,x = 2\).
Vậy nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là \[1 < x < 2\].
Câu 3
A. \[S = \left\{ 0 \right\}\].
B. \[S = \left\{ { \pm 3} \right\}\].
C. \[S = \left\{ {0\,;3} \right\}\].
D. \[S = \left\{ 3 \right\}\].
Lời giải
Bình phương hai vế của phương trình, ta có
\(2{x^2} - 3x + 5 = {x^2} + 5 \Leftrightarrow {x^2} - 3x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\).
Thay lần lượt \(x = 3\) và \(x = 0\) vào phương trình đã cho, ta thấy hai nghiệm đều thỏa mãn. Vậy tập phương trình đã cho là \[S = \left\{ {0\,;3} \right\}\].
Câu 4
A. \[ - x + 2y + 7 = 0\].
B. \[2x + y + 8 = 0\].
C. \[x - 2y - 9 = 0\].
D. \[x - 2y + 9 = 0\].
Lời giải
Đường thẳng \[d\] có một véctơ pháp tuyến là \(\vec n = \left( {1; - 2} \right)\).
Vì \[\Delta \] song song \[d\] nên \[\Delta \] nhận \(\vec n = \left( {1; - 2} \right)\) làm vectơ pháp tuyến.
Vậy phương trình tổng quát của đường thẳng \[\Delta \] là: \(1\left( {x + 5} \right) - 2\left( {y - 2} \right) = 0 \Leftrightarrow x - 2y + 9 = 0.\)
Câu 5
A. \[I\left( {2;3} \right),\,\,R = 9\].
B. \[I\left( {2; - 3} \right),\,\,R = 3\].
C. \[I\left( { - 3;2} \right),\,\,R = 3\].
D. \[I\left( { - 2;3} \right),\,\,R = 3\].
Lời giải
Đường tròn tâm \[I\left( {a\,;\,b} \right)\], bán kính \[R\] có phương trình\[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\]
Do đó đường tròn \[\left( C \right)\] đã cho có tâm và bán kính là \[I\left( {2; - 3} \right),\,\,R = 3.\]
Câu 6
A. \(\frac{{{x^2}}}{{{4^2}}} - \frac{{{y^2}}}{{{5^2}}} = - 1\).
B. \(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{16}} = 1\).
C. 
.
. D. \({y^2} = 2x\).
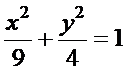Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(5!\).
B. \(C_{45}^5\).
C. \(A_{45}^5\).
D. \(45\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \({x^5} + 5{x^4}y + 10{x^3}{y^2} + 10{x^2}{y^3} + 5x{y^4} + {y^5}\).
B. \({x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
C. \({x^5} - 5{x^4}y - 10{x^3}{y^2} - 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
D. \({x^5} + 5{x^4}y - 10{x^3}{y^2} + 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[A_{35}^3\].
B. \[250\].
C. \[C_{35}^3\].
D. \(3!\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(\overline B \) là biến cố: “Số được chọn chia hết cho \(6\)”.
B. \(\overline B \) là biến cố: “Số được chọn không chia hết cho \(6\)”.
C. \(\overline B \) là biến cố: “Số được chọn chia hết cho \(3\)”.
D. \(\overline B \) là biến cố: “Số được chọn không chia hết cho \(3\)”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(\frac{{99}}{{495}}\).
B. \(\frac{{13}}{{55}}\).
C. \(\frac{{261}}{{495}}\).
D. \(\frac{{41}}{{55}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Tập nghiệm của bất phương trình \[f\left( x \right) < 0\] là \[\mathbb{R}\backslash \left( {1;3} \right)\].
Đúng
Sai
b) Tập nghiệm của bất phương trình \[f\left( x \right) \ge 0\]là \[S = \left[ {1;3} \right]\].
Đúng
Sai
c) Nghiệm \[x = 2\] là một nghiệm của bất phương trình \[f\left( x \right) > 0\].
Đúng
Sai
d) Bất phương trình \[f\left( x \right) < 2\] có tập nghiệm \[S = \mathbb{R}\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) Hypebol \(\left( H \right)\) có toạ độ tiêu điểm \[{F_1}\left( { - 5;0} \right)\,,\,\,{F_2}\left( {5;0} \right)\].
Đúng
Sai
b) Hypebol \(\left( H \right)\) có độ dài trục thực bằng \(16\).
Đúng
Sai
c) Hypebol \(\left( H \right)\) có độ dài trục ảo bằng \(4\).
Đúng
Sai
d) Hiệu các khoảng cách từ mỗi điểm nằm trên \(\left( H \right)\)đến hai tiêu điểm có giá trị tuyệt đối bằng 10.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) Có \(15\) cách lấy một quyển sách tùy ỳ từ giá sách.
Đúng
Sai
b) Có \(9\) cách lấy một quyển sách Toán hoặc Vật lý từ giá sách.
Đúng
Sai
c) Có \(10\) cách lấy hai quyển sách gồm Toán và Hóa học từ giá sách.
Đúng
Sai
d) Có \(120\) cách lấy ba quyển sách có đủ ba môn học từ giá sách.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) Xác suất để cô chủ nhiệm chọn được \[5\] học sinh nữ là \[\frac{{21}}{{15504}}\].
Đúng
Sai
b) Xác suất để cô chủ nhiệm chọn được đúng \[3\] học sinh nam là \[\frac{{C_{13}^3.C_7^2}}{{C_{20}^5}}\].
Đúng
Sai
c) Xác suất để cô chủ nhiệm chọn được ít nhất \[1\]học sinh nữ là \[\frac{{429}}{{5168}}\].
Đúng
Sai
d) Xác suất để cô chủ nhiệm số học sinh nữ nhiều hơn số học sinh nam là \[\frac{{1603}}{{7752}}\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập