Một tấm sắt hình chữ nhật có chu vi là 96 \(cm\). Người ta cắt ở mỗi góc tấm sắt một hình vuông cạnh là 4 cm.
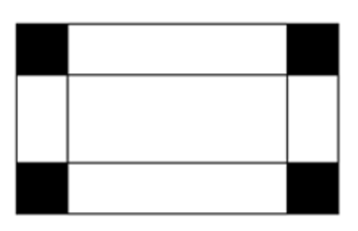
a) Diện tích phần cắt đi là \[{4.4^2}\] \[\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\]
b) Gọi chiều dài của tấm sắt là \[x\] (cm) thì chiều rộng tấm sắt là \[96 - x\] (cm)
c) Diện tích phần còn lại của tấm sắt là \[ - {x^2} + 48x - 64\,\,\left( {c{m^2}} \right)\]
d) Diện tích phần còn lại của tấm sắt ít nhất bằng 448 \(c{m^2}\) khi và chỉ khi chiều dài của tấm sắt nằm trong đoạn \([16;32]\)
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 10 cấu trúc mới (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng: Người ta cắt ở mỗi góc tấm sắt một hình vuông cạnh bằng \(4cm\) nên diện tích phần cắt đi là: \(4.4.4 = 64\,(c{m^2})\).
b) Sai: Theo bài ta có nửa chu vi của tấm sắt là \(96:2 = 48\,(cm)\)
Gọi chiều dài của tấm sắt là \(x(cm)\,\)
Chiều rộng của tấm sắt sẽ là \(48 - x\,(cm)\).
c) Đúng: Do chiều dài lớn hơn chiều rộng nên ta có:\(x > 48 - x \Leftrightarrow x > 24\,(cm)\)
Diện tích của tấm sắt ban đầu là \(x(48 - x)\,\,(c{m^2})\).
Diện tích phần còn lại của tấm sắt là \(x\left( {48 - x} \right)\, - 64 = - {x^2} + 48x - 64\,\,\left( {c{m^2}} \right)\).
d) Sai: Để diện tích còn lại của tấm sắt ít nhất bằng 448 \(c{m^2}\)nên ta có phương trình :
\(x\left( {48 - x} \right) - 64 \ge 448 \Leftrightarrow {x^2} - 48x + 512 \le 0\)
Đặt \(f\left( x \right) = {x^2} - 48x + 512\)\( \Rightarrow f(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 32\\x = 16\end{array} \right.\)
Do hệ số \(a = 1 > 0\) nên bảng xét dấu của \(f\left( x \right)\) là:
Dựa vào bảng xét dấu ta có: \(x \in \left[ {16;32} \right]\). Kết hợp với điều kiện của \(x\) ta có \(x \in (24;32]\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đúng: Số cách xếp ngẫu nhiên \(7\) học sinh không kể nam nữ lên ghế là một hoán vị của \(7\): \[{P_7} = 5040\].
b) Sai: Các học sinh cùng giới ngồi cạnh nhau, ta coi các bạn nam là nhóm A, các bạn nữ là nhóm B. Xếp \(2\) nhóm này lên ghế có: \(2! = 2\) cách.
Hoán vị \(5\) học sinh nam có: \(5! = 120\) cách
Hoán vị \(2\) học sinh nữ có: \(2! = 2\) cách
Vậy số cách xếp để học sinh cùng giới ngồi cạnh nhau là \(2.120.2 = 480\)cách.
c) Đúng: Xếp \(2\) học sinh nữ vào \(2\) đầu ghế có: \(2! = 2\) cách.
Xếp \(5\) học sinh nam vào \(5\) vị trí ở giữa có: \(5! = 120\) cách
Vậy số cách xếp để \(2\) học sinh nữ ngồi ở \(2\)đầu ghế là \(2.120 = 240\)cách.
d) Đúng: Để \(2\) học sinh nữ ngồi cạnh nhau ta coi \(2\) học sinh nữ là nhóm A.
Xếp nhóm \(A\) và \(5\) học sinh nam ghế có: \(6! = 720\) cách.
Hoán vị \(2\) học sinh nữ có: \(2! = 2\) cách
Vậy số cách xếp để \(2\) học sinh nữ ngồi cạnh nhau là \(720.2 = 1440\)cách.
Suy ra xếp \(7\) học sinh vào ghế, số cách xếp để\(2\) học sinh nữ không ngồi cạnh nhau là \[5040 - 1440 = 3600\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đúng: Số phần tử của không gian mẫu là \[n\left( \Omega \right) = C_{20}^2 = 190\].
b) Đúng: Số phần tử của biến cố lấy được hai thẻ mang số lẻ là \[C_{10}^2 = 45\].
c) Sai: Chọn hai thẻ mang số chẵn \[C_{10}^2\].
Chọn hai thẻ mang số lẻ \[C_{10}^2\].
Suy ra số phần tử của biến cố hai thẻ lấy ra có tổng chia hết cho \[2\] là \[C_{10}^2 + C_{10}^2 = 90\].
Xác suất của biến cố hai thẻ lấy ra có tổng chia hết cho \[2\] là \[\frac{{90}}{{190}} = \frac{9}{{19}}\].
d) Đúng: Chọn hai thẻ mang số chẵn \[C_{10}^2\].
Chọn một thẻ mang số chẵn và một thẻ mang số lẻ \[C_{10}^1.C_{10}^1\].
Suy ra số phần tử của biến cố hai thẻ lấy ra có tích chia hết cho \[2\] là \[C_{10}^2 + C_{10}^1.C_{10}^1 = 145\].
Xác suất của biến cố hai thẻ lấy ra có tích chia hết cho \[2\] là \[\frac{{145}}{{190}} = \frac{{29}}{{38}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập