(2,5 điểm)
Nhân dịp Lễ giỗ tổ Hùng Vương , một siêu thị điện máy đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Giá niêm yết một tủ lạnh và một máy giặt có tổng số tiền là \(25,4\)triệu đồng nhưng trong dịp này giá một tủ lạnh giảm \(40\% \) giá bán và giá một máy giặt giảm \(25\% \) giá bán nên cô Liên đã mua hai món đồ trên với tổng số tiền là \(16,77\) triệu đồng. Hỏi giá mỗi món đồ trên khi chưa giảm giá là bao nhiêu tiền ?
Quảng cáo
Trả lời:
Gọi \(x\) ( triệu đồng) là giá tiền một tủ lạnh khi chưa giảm giá \((x > 0)\)
Gọi \(y\) ( triệu đồng) là giá tiền một máy giặt khi chưa giảm giá \((y > 0)\)
Giá niêm yết hai món đồ trên là \(25,4\) triệu nên có phương trình:
\(x + y = 25,4\)
Giá bán hai món đồ trên sau khi giảm giá là \(16,77\)triệu nên có phương trình
\(\left( {100\% - 40\% } \right).x + \left( {100\% - 25\% } \right).y = 16,77\)
Giải hệ phương trình \[\left\{ \begin{array}{l}x + y = 25,4\\\frac{3}{5}x + \frac{3}{4}y = 16,77\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}x = 15,2(t/m)\\y = 10,2(t/m)\end{array} \right.\]
Vậy giá một tủ lạnh chưa giảm giá là \(15,2\) triệu đồng
Giá một máy giặt chưa giảm giá là \(10,2\)triệu đồng
Câu hỏi cùng đoạn
Câu 2:
Một người đi ô tô từ \[A\] đến \[B\] cách nhau \(100\) km với vận tốc xác định. Khi từ \[B\] trở về \[A,\] người đó đi theo đường khác dài hơn đường cũ \(20\) km nhưng với vận tốc lớn hơn vận tốc lúc đi mỗi giờ \(20\) km. Vì vậy thời gian về ít hơn thời gian đi \(30\) phút. Tính vận tốc lúc đi.
Gọi vận tốc lúc đi là \(x\) \((km,x > 0)\).
Chiều dài quãng đường đi từ A đến B là \[100km\].
Thời gian lúc đi là \(\frac{{100}}{x}\) (giờ).
Quãng đường lúc về là \(100 + 20 = 120\)(km).
Vận tốc lúc về là \(x + 20\)\[\left( {km/h} \right).\]
Thời gian lúc về là \(\frac{{120}}{{x + 20}}\)(giờ).
Vì thời gian lúc về ít hơn thời gian đi \(30\) phút \( = \frac{1}{2}\)giờ nên ta có phương trình:
\(\frac{{100}}{x} - \frac{{120}}{{x + 20}} = \frac{1}{2}\)
\( \Leftrightarrow \frac{{100\left( {x + 20} \right) - 120x}}{{x\left( {x + 20} \right)}} = \frac{1}{2}\)\( \Leftrightarrow \frac{{2000 - 20x}}{{x\left( {x + 20} \right)}} = \frac{1}{2}\)
\( \Rightarrow x\left( {x + 20} \right) = 2\left( {2000 - 20x} \right)\)\( \Leftrightarrow {x^2} + 20x = 4000 - 40x\)
\( \Leftrightarrow {x^2} + 60x - 4000 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 40\,\,\left( {tm} \right)\\x = - 100\,\,\left( {ktm} \right)\end{array} \right.\)
Vậy vận tốc lúc đi là \(40\)km/h.
Câu 3:
Cho phương trình\({x^2} - 2(m + 1)x + {m^2} + 2 = 0\)(\(x\) là ẩn số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},{\rm{ }}{x_2}\) thỏa mãn \(x_1^2 - {x_1}{x_2} + x_2^2 = 7\).
Cho phương trình \({x^2} - 2(m + 1)x + {m^2} + 2 = 0\)(\(x\)là ẩn số)
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},{\rm{ }}{x_2}\) thỏa mãn \(x_1^2 - {x_1}{x_2} + x_2^2 = 7\).
Ta có:
\(\Delta ' = {\left[ { - \left( {m + 1} \right)} \right]^2} - \left( {{m^2} + 2} \right)\)
\(\; = {m^2} + 2m + 1 - {m^2} - 2\)
\(\; = 2m - 1\)
Phương trình có hai nghiệm phân biệt khi :
\(\Delta ' > 0\)
\(2m - 1 > 0\)
\(m > \frac{1}{2}\;\;\;\left( * \right)\)
Áp dụng hệ thức Viét, ta có:
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2m + 2\;\;}\\{{x_1}{x_2} = {m^2} + 2\;\;\;\;\;\;}\end{array}} \right.\)
Theo đề bài, ta có:
\(x_1^2 - {x_1}{x_2} + x_2^2 = 7\):
\(\left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) - 3{x_1}{x_2} = 7\)
\({\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2} = 7\)
\({\left( {2m + 2} \right)^2} - 3\left( {{m^2} + 2} \right) = 7\)
\({m^2} + 8m - 9 = 0\)
\(\left( {m - 1} \right)\left( {m + 9} \right) = 0\)
\(m = 1\) hoặc \(m = - 9\)
Kết hợp (*) và (**), ta được: \(m = 1\)
Vậy \(m = 1\) là giá trị cần tìm.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
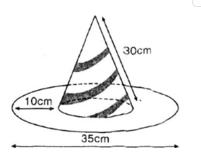
a) Bán kính đường tròn đáy của hình nón: \[r = \frac{{35 - 2.10}}{2} = 7,5\,({\rm{cm}})\]
Chiều cao của cái mũ: \[h = \sqrt {{{30}^2} - {{7,5}^2}} \approx 29(cm)\]
Tính thể tích của cái mũ: \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.7,5^2}.29 = 543,75\pi \approx 1708(c{m^3})\]
b) Diện tích giấy làm nên cái mũ là tổng diện tích xung quanh của hình nón và diện tích vành nón.
Diện tích xung quanh hình nón: \[Sxq\; = \pi .r.l = \pi .7,5.30 = 225\pi {\rm{ }}({\rm{c}}{{\rm{m}}^2})\]
Diện tích vành nón (hình vành khăn): \[{S_{vk}} = \pi .{\left( {\frac{{35}}{2}} \right)^2} - \pi {.7,5^2} = 250\pi \,({\rm{c}}{{\rm{m}}^2})\]
Diện tích tích giấy làm nên cái mũ : \[S = 225\pi + 250\pi = 475\pi {\rm{ }} \approx {\rm{ }}1492{\rm{ (c}}{{\rm{m}}^{\rm{2}}})\]
Lời giải
Nhóm \[\left[ {40\,\,;\,\,60} \right)\] có tần số tương đối là \[\frac{{11}}{{36}} \approx 30,6\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.