Cho phương trình \({x^2} + (m - 2)x + m - 3 = 0\) (\[x\] là ẩn số, \[m\]là tham số). Tìm \[m\] để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho biểu thức \(A = 2{x_1}{x_2} - {\left( {{x_1} - {x_2}} \right)^2} + 3\) đạt giá trị lớn nhất.

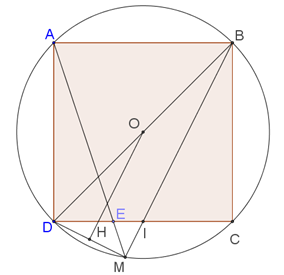
Ta có \(AD = R\sqrt 2 \); \(DE = \frac{{R\sqrt 2 }}{3}\); \(AE = \sqrt {A{D^2} + D{E^2}} = \sqrt {2{R^2} + \frac{{2{R^2}}}{9}} = \frac{{2\sqrt 5 }}{3}R\) .

Tam giác \[DOM\] cân tại \[O\] mà \[OH \bot DM\]

Suy ra

\[ \Rightarrow DH = \frac{{R\sqrt {10} }}{{10}}\] \[ \Rightarrow DM = \frac{{R\sqrt {10} }}{5}\]

Ta có  (g-g) \( \Rightarrow \frac{{ME}}{{CE}} = \frac{{DE}}{{AE}} = \frac{{MD}}{{AC}}\)

\( \Rightarrow \frac{{ME}}{{AE}}.\frac{{DE}}{{CE}} = \frac{{M{D^2}}}{{A{C^2}}} = \frac{1}{{10}}\) \( \Rightarrow \frac{{ME}}{{AE}} = \frac{1}{5} \Rightarrow \frac{{ME}}{{AM}} = \frac{1}{6}\)

\(EI{\rm{//}}AB \Rightarrow \frac{{EI}}{{AB}} = \frac{{ME}}{{AM}} = \frac{1}{6}\) \( \Rightarrow EI = \frac{1}{6}AB = \frac{{R\sqrt 2 }}{6}\)\( \Rightarrow DI = DE + EI = \frac{{R\sqrt 2 }}{3} + \frac{{R\sqrt 2 }}{6} = \frac{{R\sqrt 2 }}{2}\).

a) Tứ giác \[MNAC\] có \[\widehat {MNA} + \widehat {MCA} = {90^o} + {90^o} = {180^o}\]

nên \[MNAC\] là tứ giác nội tiếp.

\[ \Rightarrow \widehat {ACN} = \widehat {AMN}\].

b) Ta có: \[\widehat {ACN} = \widehat {AMN}\]

\[\widehat {AMN} = \widehat {ADC}\] (do MN//DC vì cùng vuông góc với AB)

\[AB \bot CD\] suy ra \[H\] là trung điểm của \[CD\].

Tam giác \[ACD\] là tam giác cân do \[AH\] vừa là đường cao, vừa là trung tuyến.

Suy ra \[\widehat {ADC} = \widehat {ACD}\]. Từ đó ta có: \[\widehat {ACN} = \widehat {ACD}\].

Ta có: \[\widehat {NCO} = \widehat {ACN} + \widehat {ACO} = \widehat {ACD} + \widehat {OAC = }{90^O}\]. Suy ra \[CN \bot CO\].

\( \Rightarrow \Delta NCO\) vuông tại \(C\) \( \Rightarrow C{H^2} = NH.OH\).

c) \[\widehat {ACE} = \widehat {EAC}\] (cùng bằng ).\( \Rightarrow \) \[\Delta AEC\] cân tại \[E\] \[ \Rightarrow E\] thuộc đường trung trực của\[AC\]. Gọi \[F = AE \cap BM\]

Ta có \[C\] thuộc đường tròn đường kính\[FA\]. Nên đường trung trực của \[AC\] phải cắt đường kính \[FA\] tại tâm của đường tròn này. Suy ra \[E\] là trung điểm của\[FA\].

Gọi \[K = CH \cap BE\]. Ta có: \[CH//FA\] nên \[\frac{{CK}}{{FE}} = \frac{{KH}}{{EA}}\left( { = \frac{{BK}}{{BE}}} \right)\].

Mà \[FE = EA\] nên \[CK = KH\]. Vậy \[BE\] đi qua trung điểm của \[CH\].