Cho \(\left( {{O_1}} \right),\,\left( {{O_2}} \right)\) là hai đường tròn, cắt nhau tại điểm \(A,\,M\), sao cho \(\widehat {{O_1}A{O_2}}\) là góc tù. Tiếp tuyến tại \(A\) của \(\left( {{O_1}} \right)\) cắt \(\left( {{O_2}} \right)\) tại điểm thứ hai \(B\) (khác \(A\)). Tiếp tuyến tại \(A\) của \(\left( {{O_2}} \right)\) cắt \(\left( {{O_1}} \right)\) tại điểm thứ hai \(D\) (khác \(A\)).
a) Trên cung \(AD\) không chứa \(M\) của \(\left( {{O_1}} \right)\), lấy điểm \(K\), khác \(A\) và \(D\), sao cho đường thẳng \(KM\) cắt cung \(AB\) không chứa \(M\) của \(\left( {{O_2}} \right)\) tại điểm \(L\), khác \(A\) và \(B\). Chứng minh rằng đường thẳng \(AK\) song song với đường thẳng \(BL\).
b) Gọi \(C\) là điểm đối xứng của \(A\) qua \(M\). Chứng minh rằng \(ABCD\) là tứ giác nội tiếp.
Cho \(\left( {{O_1}} \right),\,\left( {{O_2}} \right)\) là hai đường tròn, cắt nhau tại điểm \(A,\,M\), sao cho \(\widehat {{O_1}A{O_2}}\) là góc tù. Tiếp tuyến tại \(A\) của \(\left( {{O_1}} \right)\) cắt \(\left( {{O_2}} \right)\) tại điểm thứ hai \(B\) (khác \(A\)). Tiếp tuyến tại \(A\) của \(\left( {{O_2}} \right)\) cắt \(\left( {{O_1}} \right)\) tại điểm thứ hai \(D\) (khác \(A\)).
a) Trên cung \(AD\) không chứa \(M\) của \(\left( {{O_1}} \right)\), lấy điểm \(K\), khác \(A\) và \(D\), sao cho đường thẳng \(KM\) cắt cung \(AB\) không chứa \(M\) của \(\left( {{O_2}} \right)\) tại điểm \(L\), khác \(A\) và \(B\). Chứng minh rằng đường thẳng \(AK\) song song với đường thẳng \(BL\).
b) Gọi \(C\) là điểm đối xứng của \(A\) qua \(M\). Chứng minh rằng \(ABCD\) là tứ giác nội tiếp.
Quảng cáo
Trả lời:
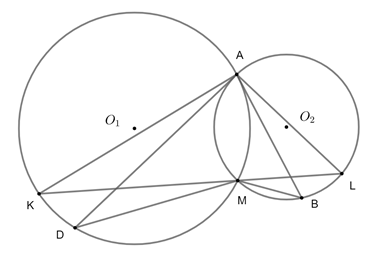
a)Với giả thuyết \(\widehat {{O_1}A{O_2}}\) là góc tù, ta có thế hình như ở trên.
Xét \(\left( {{O_1}} \right)\), ta có:
\(\widehat {AKM} = \widehat {MAB}\) (góc nọi tiếp và góc tạo bởi tiếp tuyến và một dây, cùng chắn cung AM không chứa D). (1)
Xét \(\left( {{O_2}} \right)\), ta có:
\(\widehat {MLB} = \widehat {MAB}\) (hai góc nội tiếp cùng chắn cung MB không chứa A). (2)
Từ (1) và (2), suy ra, \(\widehat {AKM} = \widehat {MLB}\).
Do đó, \(AK\,{\rm{//}}\,LB\) (vì có hai góc ở vị trí so le trong bằng nhau).
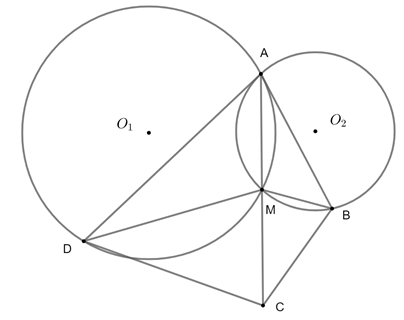
b)Xét \(\left( {{O_1}} \right)\) ta có:
\(\widehat {MDA} = \widehat {MAB}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và một dây, cùng chắn cung AM không chứa D). (3)
Xét \(\left( {{O_2}} \right)\) ta có
\(\widehat {MAD} = \widehat {MBA}\) (góc tạo bởi tiếp tuyến và một dây, góc nội tiếp, cùng chắn cung AM không chứa B) (4)
Từ (3) và (4), suy ra, .
Do đó, \(\frac{{MA}}{{MD}} = \frac{{MB}}{{MA}}\); mà \(MC = MA\)(gt), nên \(\frac{{MC}}{{MD}} = \frac{{MB}}{{MC}}\). (5)
Do trong một tam giác, mỗi góc ngoài bằng tổng hai góc trong không kề với nó, nên cộng (3) và (4), vế theo vế, ta được:
\(\widehat {DMC} = \widehat {CMB}\) (6)
Từ (5) và (6), suy ra, .
Do đó, \(\widehat {DCM} = \widehat {CBM}\).
Vì thế, ta có:
\(\begin{array}{l}\widehat {DCB} = \widehat {DCM} + \widehat {MCB} = \widehat {CBM} + \widehat {MCB}\\ = 180^\circ - \widehat {BMC} = 180^\circ - (\widehat {BAM} + \widehat {MBA})\\ = 180^\circ - (\widehat {BAM} + \widehat {MAD})\quad ({\rm{do}}(4))\\ = 180^\circ - \widehat {BAD}\end{array}\)
Suy ra, \(\widehat {BAD} + \widehat {DCB} = 180^\circ \). Do đó, \(ABCD\) là tứ giác nội tiếp.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
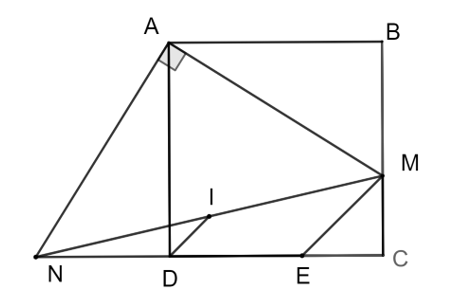
Xét hai tam giác vuông \(ABM\) và \(ADN\), ta có:
\(AB = AD\),\(\widehat {BAM} = \widehat {DAN}\) (hai góc nhọn có cạnh tương ứng vuông góc)
Do đó tam giác \(\Delta ABM = \Delta ADN\) (cạnh góc vuông – góc nhọn). Suy ra, \(DN = BM\) (1).
Qua \(M\) kẻ đường thẳng song song \(ID\) cắt \(NC\) tại \[E\].
Xét tam giác \(MNE\):
Do \(I\) là trung điểm của \(MN\) và \(ID\,{\rm{//}}\,ME\), nên \(D\) là trung điểm của \(NE\). Vì thế \(DE = DN = BM\) (theo (1)). Suy ra, \(MC = CE\) (2)
Do \(I,D\) tương ứng là trung điểm của \(MN,\,NE\), nên \(ID\) là đường trung bình của tam giác. Do đó, \(DI = \frac{1}{2}EM\).
Xét tam giác vuông (tại C) MCE, theo định lí Pitago, ta có:
\(EM = \sqrt {M{C^2} + C{E^2}} = \sqrt {2M{C^2}} \)(do (2))
\( = \sqrt 2 MC = \sqrt 2 \left( {BC - BM} \right) = \sqrt 2 \left( {8 - 5} \right) = 3\sqrt 2 \).
Vì thế \(DI = \frac{{3\sqrt 2 }}{2}\).
Lời giải
a)Vì \(m,\,p\) là các số nguyên tố nên \(mp \ge 4\). Do đó, \(r \ge 5\). Mà \(r\) là nguyên tố nên r là số lẻ.
Vì thế, \(mp = r - 1\) là một số chẵn. Suy ra, trong hai số \(m,\,p\), có ít nhất một số bằng 2.
- Nếu \(m = 2\) thì \(r = 2p + 1\). Do đó:
\({p^2} + r = {p^2} + 2p + 1 = {\left( {p + 1} \right)^2}\),
Là một số chính phương.
- Nếu \(p = 2\) thì \(r = 2m + 1\). Do đó
\({m^2} + r = {m^2} + 2m + 1 = {\left( {m + 1} \right)^2}\) là một số chính phương
b)Giả sử q là số nguyên tố thỏa mãn yêu cầu đề bài. Khi đó, sẽ tồn tại các số nguyên dương
\[n,\,k\] sao cho \({n^2} + 22q = {11^k}\). (1)
Do \({n^2} + 22q > 11\) nên \({11^k} > 11\); suy ra \(k \ge 2\). Vì thế, từ (1), ta có:
\(\left( {{n^2} + 22q} \right) \vdots {11^2}\). (2)
Do \(22q \vdots 11\) nên từ (1) suy ra, \({n^2} \vdots 11\); mà 11 là số nguyên tố, nên \({n^2} \vdots {11^2}\). (3)
Từ (2) và (3) suy ra, \(22q \vdots {11^2}\). Do đó, \[q \vdots 11\]; mà \[q\] là số nguyên tố nên \(q = 11\).
Ngược lại, với \(q = 11\), ta có: \({33^2} + 22.11 = {11^2}.\left( {9 + 2} \right) = {11^3}\).
Vậy có duy nhất số q thỏa yêu cầu của đề bài là \(q = 11\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.