Cho hình vuông \(ABCD\). Vẽ đường tròn tâm \(O\) đường kính \(BC\)và đường tròn\(\left( {A;AB} \right)\)chúng cắt nhau tại một điểm thứ hai là \(E\)( E khác B). Tia \(CE\)cắt \(AD\) tại điểm \(F.\) Chứng minh rằng \(F\)là trung điểm của\(AD\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
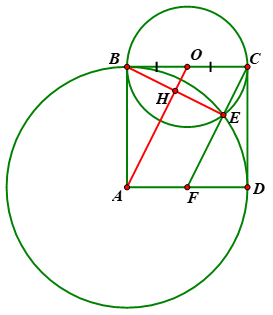
- Kẻ đoạn nối tâm OA và dây chung BE \( \Rightarrow OA \bot BE\)
- Chứng minh được: \(BE \bot CF\)
- Chứng minh được:\(OA//CF\)
- Chứng minh được tứ giác \(AOCF\) là hình bình hành\( \Rightarrow OC = FA\).
- Lập luận: từ\(OC = \frac{{BC}}{2} = \frac{{AD}}{2}\)\( \Rightarrow {\rm{AF}} = \frac{{AD}}{2} \Rightarrow \)\(F\)là trung điểm của\(AD\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
- Biến đổi được:
\[a + b + 20c = {c^3} \Leftrightarrow a + b + c = {c^3} - c - 18c\]
\[ \Leftrightarrow a + b + c = c\left( {c - 1} \right)\left( {c + 1} \right) - 18c\]
- Chứng minh được:\[ \Leftrightarrow a + b + c = c\left( {c - 1} \right)\left( {c + 1} \right) - 18c \vdots 6\]
- Mặt khác: \[{a^3} + {b^3} + {c^3} - (a + b + c)\]
\[ = (a - 1)a(a + 1) + (b - 1)b(b + 1) + (c - 1)c(c + 1) \vdots 6\]
- Lập luận kết luận \[{a^3} + {b^3} + {c^3}\] chia hết cho 6.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Với \[a,b > 0\], ta chứng minh \[\frac{{{a^3}}}{{{a^2} + {b^2}}} \ge a - \frac{b}{2}\].
- Áp dụng: \({\left( {a - b} \right)^2} \ge 0 \Leftrightarrow {a^2} + {b^2} \ge 2ab \Leftrightarrow \frac{{ - 1}}{{{a^2} + {b^2}}} \ge \frac{{ - 1}}{{2ab}}\)
Khi đó:
\[\frac{{{a^3}}}{{{a^2} + {b^{^2}}}} = \frac{{a({a^2} + {b^2}) - a{b^2}}}{{{a^2} + {b^2}}} = a - \frac{{a{b^2}}}{{{a^2} + {b^2}}} \ge a - \frac{{a{b^2}}}{{2ab}} = a - \frac{b}{2}\]
\[ \Rightarrow \frac{{{b^3}}}{{{b^2} + {c^2}}} \ge b - \frac{c}{2}\] \[;\frac{{{c^3}}}{{{c^2} + {a^2}}} \ge c - \frac{a}{2}\]
Cộng vế theo vế ba bất đẳng thức trên ta có:
\[\frac{{{a^3}}}{{{a^2} + {b^2}}} + \frac{{{b^3}}}{{{b^2} + {c^2}}} + \frac{{{c^3}}}{{{c^2} + {a^2}}} \ge \frac{{a + b + c}}{2}\]
- Áp dụng:\({\left( {a - b} \right)^2} \ge 0 \Leftrightarrow 2\left( {{a^2} + {b^2}} \right) \ge 4ab\)
Ta có:
\[\frac{{{a^3}}}{{{a^2} + 4ab + {b^2}}} \ge \frac{{{a^3}}}{{{a^2} + 2({a^2} + {b^2}) + {b^2}}} = \frac{1}{3}.\frac{{{a^3}}}{{{a^2} + {b^2}}}\];\[\frac{{{b^3}}}{{{b^2} + 4bc + {c^2}}} \ge \frac{{{b^3}}}{{{b^2} + 2({b^2} + {c^2}) + {c^2}}} = \frac{1}{3}.\frac{{{b^3}}}{{{b^2} + {c^2}}}\];\[\frac{{{c^3}}}{{{c^2} + 4ac + {a^2}}} \ge \frac{{{c^3}}}{{{c^2} + 2({c^2} + {a^2}) + {a^2}}} = \frac{1}{3}.\frac{{{c^3}}}{{{c^2} + {a^2}}}\]
Cộng vế theo vế ba bất đẳng thức trên ta có:
\[\begin{array}{l}\frac{{{a^3}}}{{{a^2} + 4ab + {b^2}}} + \frac{{{b^3}}}{{{b^2} + 4bc + {c^2}}} + \frac{{{c^3}}}{{{c^2} + 4ca + {a^2}}}\\ \ge \frac{1}{3}\left( {\frac{{{a^3}}}{{{a^2} + {b^2}}} + \frac{{{b^3}}}{{{b^2} + {c^2}}} + \frac{{{c^3}}}{{{c^2} + {a^2}}}} \right) \ge \frac{{a + b + c}}{6} = 1\end{array}\]
-Vậy giá trị nhỏ nhất của P là 1, dấu “=” xảy ra khi \[a = b = c = 2.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập