khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Ôn vào 10
  3. Toán

Câu hỏi:

10/01/2026 313 Lưu

Cho Parabol là đồ thị hàm số \(y =  - \frac{1}{2}{x^2}\) và đường thẳng d là đồ thị hàm số \(y = mx + m - 1\) (với m là tham số).

          a. Vẽ Parabol là đồ thị hàm số \(y =  - \frac{1}{2}{x^2}\).

          b. Chứng minh Parabol luôn cắt đường thẳng d tại hai điểm phân biệt với mọi giá trị của tham số m.

Xem lời giải

Câu hỏi trong đề: Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 chuyên Lê Quý Đôn - Lai Châu có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a)

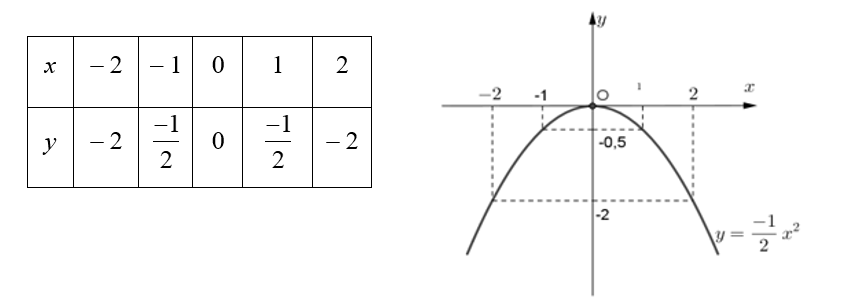
Cho Parabol là đồ thị hàm số y = -1/2 x ^2 (ảnh 1)

b. Xét phương trình hoành độ giao điểm của (d)  và (P):

\( - \frac{1}{2}{x^2}\)=\(mx + m - 1\)\( \Leftrightarrow {x^2} + 2mx + 2m - 2 = 0{\rm{  }}\left( 1 \right)\)

Phương trình (1) có \(\Delta ' = {m^2} - 2m + 2 = {(m - 1)^2} + 1 > 0\) với mọi m. Phương trình (1) luôn có hai nghiệm phân biệt. Do đó (d) luôn cắt (P) tại hai điểm phân biệt.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn tâm (O; R), từ một điểm A trên đường tròn kẻ tiếp tuyến d  với đường tròn tâm O. Trên đường thẳng d lấy điểm M  bất kì (M khác A), kẻ tiếp tuyến thứ hai MB (B là tiếp điểm).

a. Chứng minh tứ giác AMBO là tứ giác nội tiếp đường tròn.

b. Gọi I  là giao điểm của AB và OM. Chứng minh  \(OI.OM = {R^2};{\rm{ }}OI.IM = \frac{{A{B^2}}}{4}\).

c. Gọi điểm H là trục tâm của tam giác MAB. Tìm quỹ tích điểm H khi điểm M di chuyển trên đường thẳng d.

Lời giải

Cho đường tròn tâm (O; R), từ một điểm A trên đường tròn kẻ tiếp tuyến d  với đường tròn tâm O. (ảnh 1)

a. Vì MA, MB là tiếp truyến của đường tròn (O) \( \Rightarrow \widehat {MAO} = 90^\circ ;\widehat {MBO} = 90^\circ \).

Ta có: \(\widehat {MAO} + \widehat {MBO} = 180^\circ \).

\( \Rightarrow AMBO\) nội tiếp đường tròn đường kính OM.

b. Ta có MA = MB (tính chất 2 tiếp tuyến cắt nhau) và OA = OB = R.

\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB \( \Rightarrow OM \bot AB\) tại I.

Ta lại có: \(\widehat {MAO} = 90^\circ \)(tính chất của tiếp tuyến)

\( \Rightarrow \Delta MAO\) vuông tại A.

Áp dụng hệ thức lượng trong tam giác vuông ta có:

\(OI.OM = O{A^2} = {R^2}\)  và \(OI.{\rm{ }}IM = I{A^2} = \frac{{A{B^2}}}{4}\) (đpcm).

c.    Ta có: \(OB \bot MB\) (tính chất của tiếp tuyến) và \(AK \bot MB\)(AK là đường cao của \(\Delta MAB\)).

\( \Rightarrow OB//AK{\rm{ hay }}OB//AH{\rm{  }}(1)\).

Chứng minh tương tự ta có: \(OA//BN{\rm{ hay }}OA//BH{\rm{  }}(2)\).

Từ (1) và (2) suy ra: tứ giác AOBN là hình bình hành.

Mà OA = OA = R.

\( \Rightarrow \) hình bình hành AOBN là hình thoi.

\( \Rightarrow \) AH = AO = R

Vậy khi M  di chuyển trên đường thẳng (d) thì H luôn cách A cố định một khoảng bằng R. Do đó, quỹ tích của điểm H khi M di chuyển trên đường thẳng (d) là nửa đường tròn tâm (A; AH), AH = R.

Câu 2

Một ô tô khách và một ô tô tải chở vật liệu xây dựng khởi hành cùng một lúc từ bến xe khách Lai Châu đến trung tâm thị trấn Mường Tè. Do trọng tải lớn nên xe tải chở vật liệu xây dựng đi với vận tốc chậm hơn xe khách 10 km/h. Xe khách đến trung tâm thị trấn Mường Tè sớm hơn xe tải 1 giờ 6 phút. Tính vận tốc mỗi xe biết quãng đường từ bến xe khách thành phố Lai Châu đến trung tâm thị trấn Mường Tè là 132 km.

Lời giải

Gọi vận tốc của xe tải là x (km/h) (x > 0)

Suy ra, vận tốc của xe khách là x +10 (km/h)

Thời gian đi hết quãng đường của xe tải là \(\frac{{132}}{x}\left( h \right)\) và xe khách là \(\frac{{132}}{{x + 10}}\left( h \right)\)

Vì xe khách đi nhanh hơn xe tải là 1 giờ 6 phút = \(\frac{{11}}{{10}}\left( h \right)\)  

Nên ta có phương trình:

 \(\begin{array}{l}\frac{{132}}{x} - \frac{{132}}{{x + 10}} = \frac{{11}}{{10}}\\ \Rightarrow 132.10\left( {x + 10} \right) - 132.10x = 11x\left( {x + 10} \right)\\ \Leftrightarrow {x^2} + 10x - 1200 = 0\end{array}\)

Giải phương trình ta được x1 = – 40 (loại); x2 = 30 (thỏa mãn)

Vậy vận tốc của xe tải là 30 km/h và xe khách là 40 km/h.

Câu 3

Giải phương trình sau: \(\left( {2x + 5} \right)\sqrt {2x + 5}  = {x^2} + 7x + 5.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải các phương trình và hệ phương trình:

a. \[5x--10 = 0\]               b. \[{x^2} + 6x + 5 = 0\]                     \({\bf{c}}.{\rm{ }}\left\{ \begin{array}{l}2x + y = 4\\x - y = 8\end{array} \right.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

1. Thực hiện phép tính sau: \(\sqrt 3 - \sqrt {48} + \sqrt {75} \)

2.Cho biểu thức \({\rm{P}} = \left( {\frac{{\sqrt x }}{{\sqrt x + 3}} + \frac{3}{{\sqrt x - 3}}} \right):\frac{{x - 9}}{{\sqrt x + 3}}\) (với \(x \ge 0;x \ne 9)\).

a. Rút gọn biểu thức \[{\rm{P}}\].

b. Tính giá trị của \[{\rm{P}}\]khi \[x = 16\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập