Cho đường tròn tâm (O; R), từ một điểm A trên đường tròn kẻ tiếp tuyến d với đường tròn tâm O. Trên đường thẳng d lấy điểm M bất kì (M khác A), kẻ tiếp tuyến thứ hai MB (B là tiếp điểm).
a. Chứng minh tứ giác AMBO là tứ giác nội tiếp đường tròn.
b. Gọi I là giao điểm của AB và OM. Chứng minh \(OI.OM = {R^2};{\rm{ }}OI.IM = \frac{{A{B^2}}}{4}\).
c. Gọi điểm H là trục tâm của tam giác MAB. Tìm quỹ tích điểm H khi điểm M di chuyển trên đường thẳng d.
Cho đường tròn tâm (O; R), từ một điểm A trên đường tròn kẻ tiếp tuyến d với đường tròn tâm O. Trên đường thẳng d lấy điểm M bất kì (M khác A), kẻ tiếp tuyến thứ hai MB (B là tiếp điểm).
a. Chứng minh tứ giác AMBO là tứ giác nội tiếp đường tròn.
b. Gọi I là giao điểm của AB và OM. Chứng minh \(OI.OM = {R^2};{\rm{ }}OI.IM = \frac{{A{B^2}}}{4}\).
c. Gọi điểm H là trục tâm của tam giác MAB. Tìm quỹ tích điểm H khi điểm M di chuyển trên đường thẳng d.Quảng cáo
Trả lời:
Giải bởi Vietjack
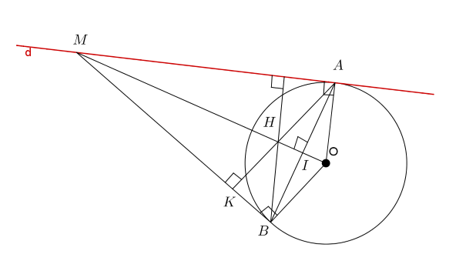
a. Vì MA, MB là tiếp truyến của đường tròn (O) \( \Rightarrow \widehat {MAO} = 90^\circ ;\widehat {MBO} = 90^\circ \).
Ta có: \(\widehat {MAO} + \widehat {MBO} = 180^\circ \).
\( \Rightarrow AMBO\) nội tiếp đường tròn đường kính OM.
b. Ta có MA = MB (tính chất 2 tiếp tuyến cắt nhau) và OA = OB = R.
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB \( \Rightarrow OM \bot AB\) tại I.
Ta lại có: \(\widehat {MAO} = 90^\circ \)(tính chất của tiếp tuyến)
\( \Rightarrow \Delta MAO\) vuông tại A.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(OI.OM = O{A^2} = {R^2}\) và \(OI.{\rm{ }}IM = I{A^2} = \frac{{A{B^2}}}{4}\) (đpcm).
c. Ta có: \(OB \bot MB\) (tính chất của tiếp tuyến) và \(AK \bot MB\)(AK là đường cao của \(\Delta MAB\)).
\( \Rightarrow OB//AK{\rm{ hay }}OB//AH{\rm{ }}(1)\).
Chứng minh tương tự ta có: \(OA//BN{\rm{ hay }}OA//BH{\rm{ }}(2)\).
Từ (1) và (2) suy ra: tứ giác AOBN là hình bình hành.
Mà OA = OA = R.
\( \Rightarrow \) hình bình hành AOBN là hình thoi.
\( \Rightarrow \) AH = AO = R
Vậy khi M di chuyển trên đường thẳng (d) thì H luôn cách A cố định một khoảng bằng R. Do đó, quỹ tích của điểm H khi M di chuyển trên đường thẳng (d) là nửa đường tròn tâm (A; AH), AH = R.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi vận tốc của xe tải là x (km/h) (x > 0)
Suy ra, vận tốc của xe khách là x +10 (km/h)
Thời gian đi hết quãng đường của xe tải là \(\frac{{132}}{x}\left( h \right)\) và xe khách là \(\frac{{132}}{{x + 10}}\left( h \right)\)
Vì xe khách đi nhanh hơn xe tải là 1 giờ 6 phút = \(\frac{{11}}{{10}}\left( h \right)\)
Nên ta có phương trình:
\(\begin{array}{l}\frac{{132}}{x} - \frac{{132}}{{x + 10}} = \frac{{11}}{{10}}\\ \Rightarrow 132.10\left( {x + 10} \right) - 132.10x = 11x\left( {x + 10} \right)\\ \Leftrightarrow {x^2} + 10x - 1200 = 0\end{array}\)
Giải phương trình ta được x1 = – 40 (loại); x2 = 30 (thỏa mãn)
Vậy vận tốc của xe tải là 30 km/h và xe khách là 40 km/h.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a)
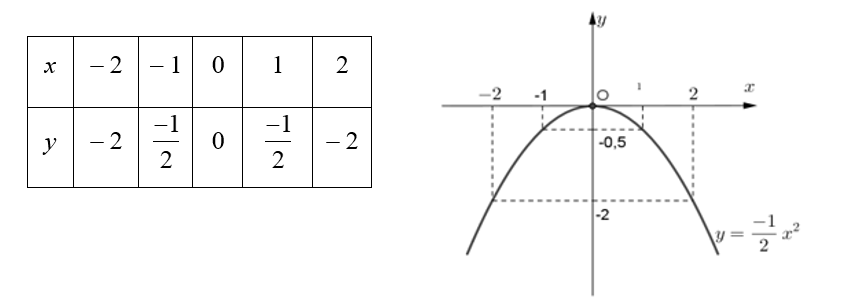
b. Xét phương trình hoành độ giao điểm của (d) và (P):
\( - \frac{1}{2}{x^2}\)=\(mx + m - 1\)\( \Leftrightarrow {x^2} + 2mx + 2m - 2 = 0{\rm{ }}\left( 1 \right)\)Phương trình (1) có \(\Delta ' = {m^2} - 2m + 2 = {(m - 1)^2} + 1 > 0\) với mọi m. Phương trình (1) luôn có hai nghiệm phân biệt. Do đó (d) luôn cắt (P) tại hai điểm phân biệt.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập