Cho \(A = 2\sqrt {18} - 2\sqrt 8 \) và \(B = 2\sqrt[3]{8} + \sqrt[3]{{ - 27}}\). Tính giá trị của biểu thức \(P = {A^2} - B.\)

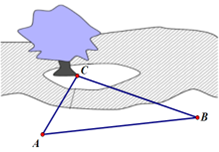
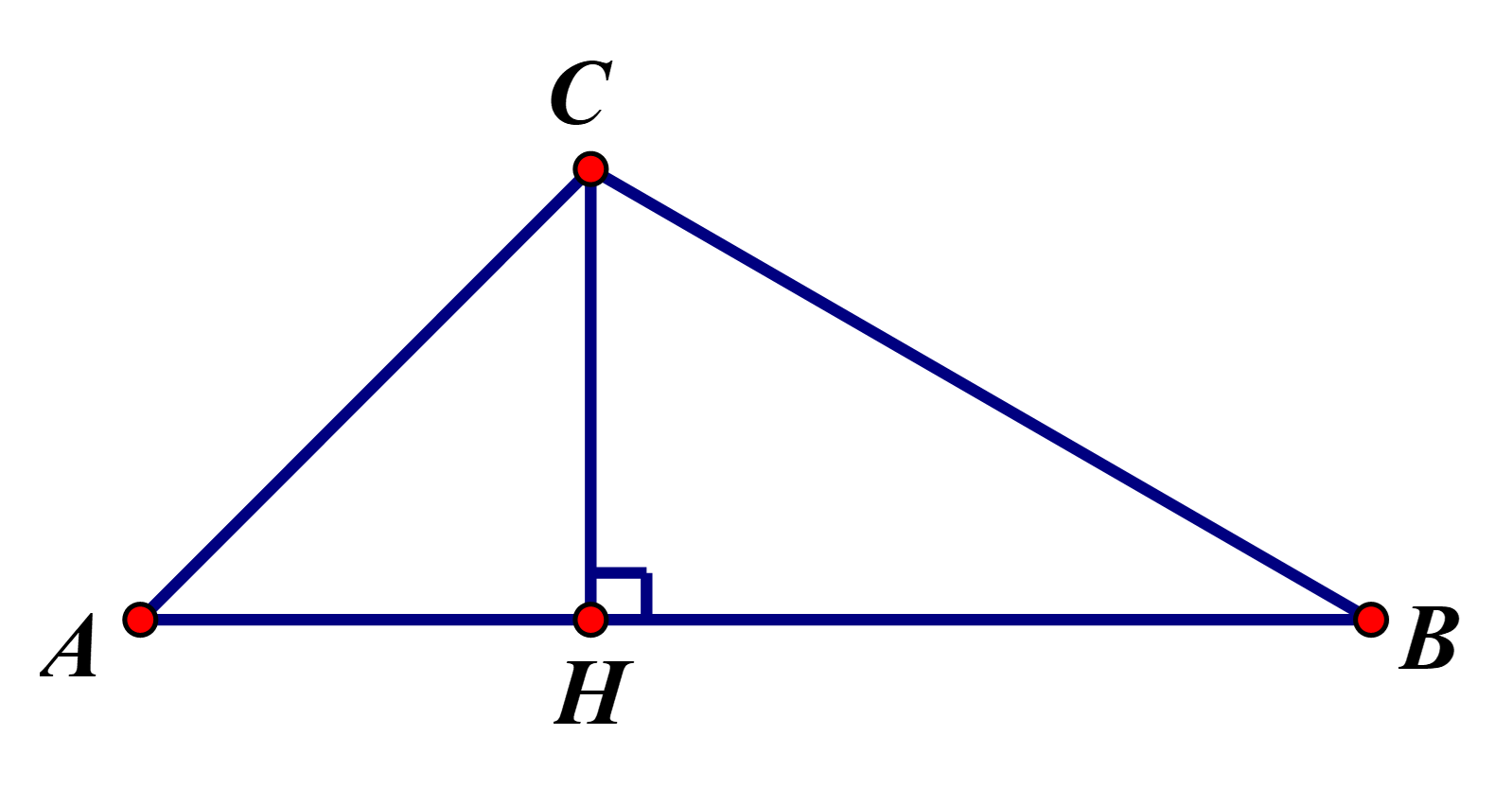
Gọi H là chân đường cao kẻ từ \(C\) đến \(AB\) của \(\Delta ABC\)

\(\Delta AHC\) vuông cân tại \(H\) nên ta có \(HA = HC.\)

\(\Delta BHC\) vuông tại \(H\) nên ta có \(HB = CH.\cot B = CH.\cot 30^\circ = \sqrt 3 .CH\)

Mà \(AH + HB = AB\) hay \(HC + \sqrt 3 .CH = 60\)

\(HC = \frac{{60}}{{1 + \sqrt 3 }}.\)

Do \(\Delta BHC\) vuông tại \(H\) nên \(BC = \frac{{HC}}{{\sin B}} = \frac{{60}}{{\left( {1 + \sqrt 3 } \right).\sin 30^\circ }} = 60\left( {\sqrt 3 - 1} \right)\,\,\left( m \right).\)

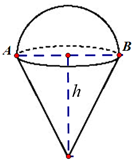
Bán kính đường tròn đáy hình nón là \(R = \frac{{AB}}{2} = 25\left( {cm} \right)\)

Thể tích khối nón là \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.25^2}.120 = 25000\pi \left( {c{m^3}} \right)\)

Vì \(R = 25\,cm\) cũng là bán kính của nửa mặt cầu.

nên thể tích của nửa khối cầu phần trên là \({V_{nc}} = \frac{1}{2}.\frac{4}{3}.\pi {R^3} = \frac{2}{3}{.25^3}\pi = \frac{{31250\pi }}{3}\left( {c{m^3}} \right)\)

Vậy thể tích của mô hình chiếc kem là

\(V = {V_n} + {V_{nc}} = 25000\pi + \frac{{31250\pi }}{3} = \frac{{106250}}{3}\pi \left( {c{m^3}} \right)\)