Một nhóm có \(5\) học sinh gồm \(3\) học sinh nam và \(2\) học sinh nữ chuẩn bị thuyết trình về chủ đề bài học. Cô giáo chọn ngẫu nhiên hai bạn của nhóm đó lên thuyết trình trước lớp. Tính xác suất của biến cố \(A\): "Hai học sinh được chọn có cả học sinh nam và học sinh nữ".
Một nhóm có \(5\) học sinh gồm \(3\) học sinh nam và \(2\) học sinh nữ chuẩn bị thuyết trình về chủ đề bài học. Cô giáo chọn ngẫu nhiên hai bạn của nhóm đó lên thuyết trình trước lớp. Tính xác suất của biến cố \(A\): "Hai học sinh được chọn có cả học sinh nam và học sinh nữ".
Quảng cáo
Trả lời:
Giả sử \(3\) học sinh nam là \(A,B,C\) và \(2\) học sinh nữ là \(M,N\).
Các trường hợp chọn ra \(2\) bạn trong \(5\) bạn \(A,B,C,M,N\)gồm: \(\left( {A,B} \right);\left( {A,C} \right);\left( {A,M} \right);\left( {A,N} \right);\left( {B,C} \right);\left( {B,M} \right);\left( {B,N} \right);\left( {C,M} \right);\left( {C,N} \right);\left( {M,N} \right)\)
Vậy có tất cả \(10\) cách chọn ra \(2\) bạn bất kì hay số phần tử của không gian mẫu là \(n\left( \Omega \right) = 10\)
Các trường hợp chọn ra \(2\) bạn trong đó có \(1\) bạn nam và \(1\) bạn nữ là:
\(\left( {A,M} \right);\left( {A,N} \right);\left( {B,M} \right);\left( {B,N} \right);\left( {C,M} \right);\left( {C,N} \right)\)
Suy ra có \(6\) cách chọn ra \(2\) bạn trong đó có \(1\) bạn nam và \(1\) bạn nữ hay số phẩn tử thuận lợi của biến cố là \(n\left( A \right) = 6\)
Vậy xác suất để chọn ra \(2\)bạn sao cho có \(1\) nam và \(1\) nữ là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{6}{{10}} = \frac{3}{5}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số phần quà tặng lớp 9A gói theo kế hoạch là \(a\) ( phần quà) ĐK \(a > 0\)
Thời gian làm số phần quà làm theo kế hoạch là : \(\frac{{600}}{a}\) (giờ)
số phần quà tặng lớp 9A gói theo thực tế là : \(a + 30\)( phần quà )
Thời gian làm số phần quà làm theo thực tế là : \(\frac{{600}}{{a + 30}}\) (giờ)
Theo giải thiết lập được phương trình : \(\frac{{600}}{a} - \frac{{600}}{{a + 30}} = 1\).
Rút gọn, quy đồng thu gọn được : \({a^2} + 30a - 1800 = 0\)
Phương trình có hai nghiệm phân biệt : \(a = 120\left( {t/m} \right)\);\(a = - 150\left( {ktm} \right)\)
Vậy theo kế hoạch, mỗi giờ lớp 9A phải gói \(120\) phần quà tặng
Lời giải
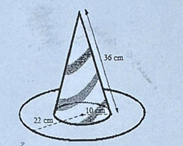
Tổng diện tích làm chiếc mũ chú hề bằng diện tích của phần thân mũ (diện tích xung quanh hình nón) và diện tích phần vành mũ (diện tích hình vành khuyên).
Diện tích của phần thân mũ là: \({S_{th\^a n}} = \pi rl \approx 3,141 \cdot 10 \cdot 36 \approx 1130,76\left( {c{m^2}} \right)\)
Diện tích phần vành mũ là: \({S_{v\`a nh}} = \pi \left( {{R^2} - {r^2}} \right) \approx 3,141 \cdot \left( {{{22}^2} - {{10}^2}} \right) \approx 1206,14\left( {c{m^2}} \right)\)
Tổng diện tích giấy làm chiếc mũ chú hề là: \(S = 1130,76 + 1206,144 = 2336,904 \approx 2337\left( {c{m^2}} \right)\).
Vậy tổng diện tích giấy làm chiếc mũ chú hề là khoảng \(2337\left( {c{m^2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.