Cho tam giác nhọn \(ABC\) (với \(AB < AC\)) có hai đường cao \(BE,CF\) cắt nhau tại điểm \(H\).
1) Chứng minh tứ giác \(AEHF\) nội tiếp đường tròn.
2) Gọi \(I\) là giao điểm của hai đường thẳng \(AH\) và \(EF\). Chứng minh rằng \(IA \cdot IH = IE \cdot IF\).
3) Gọi \(M\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng đi qua điểm \(H\) vuông góc với \(AM\), cắt cung nhỏ của đường tròn đường kính \(BC\) tại điểm \(K\). Chứng minh \(AK\) là tiếp tuyến của đường tròn đường kính \(BC\).
Cho tam giác nhọn \(ABC\) (với \(AB < AC\)) có hai đường cao \(BE,CF\) cắt nhau tại điểm \(H\).
1) Chứng minh tứ giác \(AEHF\) nội tiếp đường tròn.
2) Gọi \(I\) là giao điểm của hai đường thẳng \(AH\) và \(EF\). Chứng minh rằng \(IA \cdot IH = IE \cdot IF\).
3) Gọi \(M\) là trung điểm của đoạn thẳng \(BC\). Đường thẳng đi qua điểm \(H\) vuông góc với \(AM\), cắt cung nhỏ của đường tròn đường kính \(BC\) tại điểm \(K\). Chứng minh \(AK\) là tiếp tuyến của đường tròn đường kính \(BC\).
Quảng cáo
Trả lời:
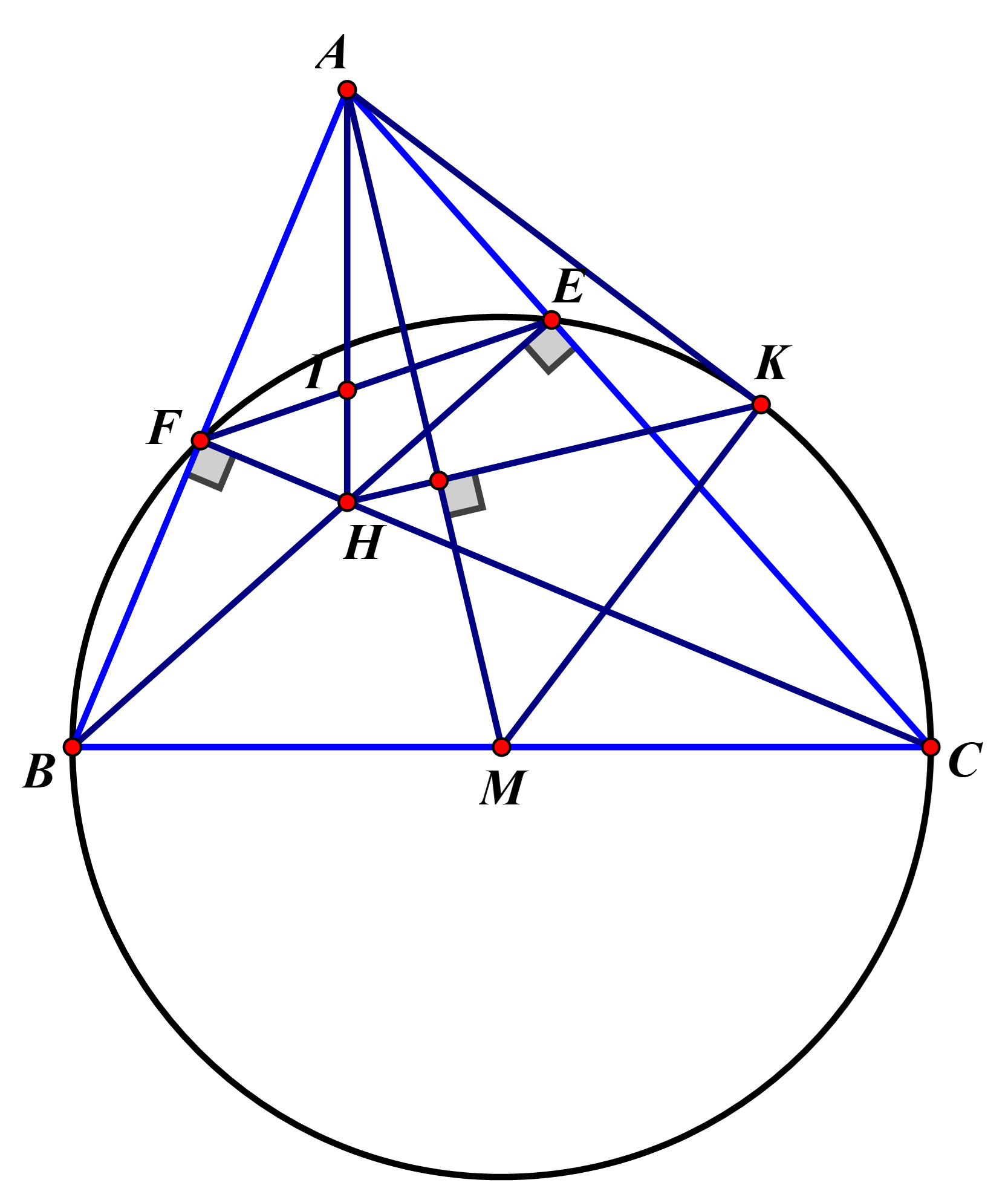
1) Do \(BE \bot AC\) nên \(\Delta AEH\)vuông tại \(E\)
Suy ra: 3 điểm \(A,E,H\)thuộc đường tròn đường kính \(AH\)
Do \(CF \bot AB\) nên \(\Delta AFH\)vuông tại \(F\)
Suy ra: 3 điểm \(A,F,H\)thuộc đường tròn đường kính \(AH\)
Suy ra: Tứ giác \(AEHF\) nội tiếp đường tròn
2) Xét \(\Delta FIH\) và \(\Delta AIE\)có:
\(\widehat {FHI} = \widehat {IEA}\) (góc nội tiếp chắn )
\(\widehat {FIH} = \widehat {EIA}\)(hai góc đối đỉnh)
Do đó
Suy ra \(\frac{{IF}}{{IA}} = \frac{{IH}}{{IE}}\) hay \(IA \cdot IH = IE \cdot IF\).
3) Gọi \(M\) là trung điểm của \(BC\), \(N\) là trung điểm \(AH\) và \(P\) là giao điểm \(HK\) với \(AM\).
Do \(\Delta BFC\) vuông tại \(F\) nên \(B,F,C\) cùng thuộc \(\left( M \right)\)
\(\Delta BEC\) vuông tại \(E\) nên \(B,E,C\) cùng thuộc \(\left( M \right)\)
Kết hợp \(K\) thuộc \(\left( M \right)\)nên \(B,C,E,F,K\) cùng thuộc \(\left( M \right)\)
Do \(HP \bot AM\) (gt) nên \(\Delta AHP\) vuông tại \(P\) nên \(P\) thuộc đường tròn đường kính \(AH\).
Do \(N\) là trung điểm \(AH\) nên \(N\) là tâm đường tròn qua \(A,E,F,P,H\).
Vì \(\Delta ABC\) có đường cao \(BE,CF\)cắt nhau tại \(H\) nên \(H\) là trực tâm.
Suy ra \(AH \bot BC\)tại \(D\)
Khi đó: \(\widehat {NEM} = 180^\circ - \left( {\widehat {NEA} + \widehat {MEC}} \right)\)\( = 180^\circ - \left( {\widehat {NEA} + \widehat {MCE}} \right)\)\( = 180^\circ - 90^\circ = 90^\circ \)
Suy ra \(\widehat {MEP} = 90^\circ - \widehat {PEN} = 90^\circ - \frac{{180^\circ - \widehat {ENP}}}{2}\) (do \(\Delta NEP\)cân tại \(N\) và tổng ba góc bằng 180°)
\( = 90^\circ - 90^\circ + \frac{1}{2}\widehat {ENP} = \widehat {EAP}\) (cùng chắn )
Vậy \(\widehat {MEP} = \widehat {EAM}\)
Xét \(\Delta MEP\) và \(\Delta MAE\) có
\[\widehat {MEP} = \widehat {EAM}\]và \(\widehat {EMA}\) chung
Suy ra
Khi đó \[\frac{{ME}}{{MA}} = \frac{{EP}}{{ME}}\]hay \[MP.MA = M{E^2}\]
Mà \[ME = MK = {R_{\left( M \right)}}\] nên \[MP.MA = M{K^2}\] hay \[\frac{{MK}}{{MA}} = \frac{{MP}}{{MK}}\]
Xét \[\Delta MKP\]và \[\Delta MAK\] có \[\frac{{MK}}{{MA}} = \frac{{MP}}{{MK}}\] và \(\widehat {MKA}\) chung nên
Suy ra \(\widehat {MPK}\)= \(\widehat {MKA}\) = 90° hay \(MK \bot AK\) nên \(AK\) là tiếp tuyến của đường tròn đường kính \(BC\)(đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số phần quà tặng lớp 9A gói theo kế hoạch là \(a\) ( phần quà) ĐK \(a > 0\)
Thời gian làm số phần quà làm theo kế hoạch là : \(\frac{{600}}{a}\) (giờ)
số phần quà tặng lớp 9A gói theo thực tế là : \(a + 30\)( phần quà )
Thời gian làm số phần quà làm theo thực tế là : \(\frac{{600}}{{a + 30}}\) (giờ)
Theo giải thiết lập được phương trình : \(\frac{{600}}{a} - \frac{{600}}{{a + 30}} = 1\).
Rút gọn, quy đồng thu gọn được : \({a^2} + 30a - 1800 = 0\)
Phương trình có hai nghiệm phân biệt : \(a = 120\left( {t/m} \right)\);\(a = - 150\left( {ktm} \right)\)
Vậy theo kế hoạch, mỗi giờ lớp 9A phải gói \(120\) phần quà tặng
Lời giải
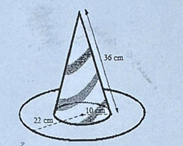
Tổng diện tích làm chiếc mũ chú hề bằng diện tích của phần thân mũ (diện tích xung quanh hình nón) và diện tích phần vành mũ (diện tích hình vành khuyên).
Diện tích của phần thân mũ là: \({S_{th\^a n}} = \pi rl \approx 3,141 \cdot 10 \cdot 36 \approx 1130,76\left( {c{m^2}} \right)\)
Diện tích phần vành mũ là: \({S_{v\`a nh}} = \pi \left( {{R^2} - {r^2}} \right) \approx 3,141 \cdot \left( {{{22}^2} - {{10}^2}} \right) \approx 1206,14\left( {c{m^2}} \right)\)
Tổng diện tích giấy làm chiếc mũ chú hề là: \(S = 1130,76 + 1206,144 = 2336,904 \approx 2337\left( {c{m^2}} \right)\).
Vậy tổng diện tích giấy làm chiếc mũ chú hề là khoảng \(2337\left( {c{m^2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.