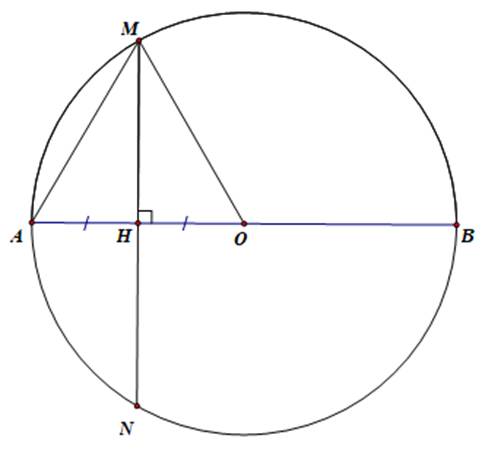
Hình vẽ bên minh họa một phần con sông có bề rộng \(AB = 100\,{\rm{m}}.\) Một chiếc thuyền đi thẳng từ vị trí \(B\) bên này bờ sông đến vị trí \(C\) bên kia bờ sông. Hỏi khoảng cách \(BC\) bằng bao nhiêu mét (kết quả được làm tròn đến hàng phần mười), biết \(AB \bot AC\) và \(\widehat {ABC} = 30^\circ ?\)

Vì phương trình \({x^2} - 7x + 5 = 0\) có hai nghiệm là \({x_1},\,\,{x_2}\) nên theo định lý Viète, ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 7\\{x_1}{x_2} = 5.\end{array} \right.\)

Vì \({x_2}\) là nghiệm của phương trình \({x^2} - 7x + 5 = 0\) nên \(x_2^2 - 7{x_2} + 5 = 0.\) Do đó \(x_2^2 - 6{x_2} + 9 = {x_2} + 4,\) hay \({\left( {{x_2} - 3} \right)^2} = {x_2} + 4.\) Suy ra \(\left| {{x_2} - 3} \right| = \sqrt {{x_2} + 4} .\)

\(P = \left| {{x_2} - 3} \right| + \sqrt {{x_1} + 4}  = \sqrt {{x_2} + 4}  + \sqrt {{x_1} + 4}  = \sqrt {{{\left( {\sqrt {{x_2} + 4}  + \sqrt {{x_1} + 4} } \right)}^2}} \)

                                  \(\begin{array}{l} = \sqrt {\left( {{x_1} + {x_2}} \right) + 8 + 2\sqrt {4\left( {{x_1} + {x_2}} \right) + {x_1}.{x_2} + 16} } \\ = \sqrt {15 + 2\sqrt {4.7 + 5 + 16} }  = \sqrt {29} .\end{array}\)A

\(A = \left( {\frac{{ - 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} + \frac{{\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right):\frac{{2\sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}\)

\[ = \frac{{\sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} \cdot \frac{{{\rm{ }}\sqrt x  + 1}}{2}\]

\[ = \frac{1}{{\sqrt x  + 1}}\,\, \cdot \frac{{{\rm{ }}\sqrt x  + 1}}{2}\]

\[ = \frac{{\sqrt x  + 1}}{{2\left( {\sqrt x  + 1} \right)}}\, = \frac{1}{2}.\]