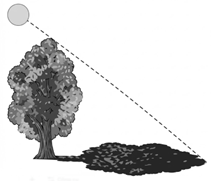
Tại thời điểm tia nắng chiếu xuống mặt đất tạo với mặt đất một góc \(40^\circ \) thì chiều dài bóng cây đo được là \(25m\) (minh họa bằng hình vẽ), giả sử cây thẳng đứng và mặt đất phẳng. Hỏi cây cao bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

Quảng cáo
Trả lời:
Đáp án đúng là C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
|
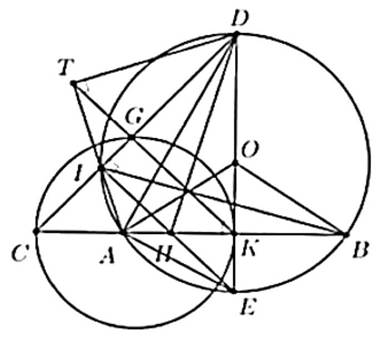
a) Chứng minh tứ giác \(DIHK\) nội tiếp đường tròn. |
|
Ta có có \(\widehat {DIE} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) |
|
\(\Delta \,DKH\) vuông tại\[K\] nên \(D,K,H\) cùng thuộc đường tròn đường kính \[DH\] |
|
\(\Delta \,DIH\) vuông tại \[I\]nên \(D,I,H\) cùng thuộc đường tròn đường kính \[DH\] |
|
Vậy \(D,I,H,K\) cùng thuộc đường tròn đường kính \[DH\]hay tứ giác \[DIHK\]nội tiếp đường tròn.
|
|
b) Chứng minh \(CI.CD = CH.CK\) và \(HA.IB = HB.IA\). |
|
Xét và có \(\widehat {DCK}\) chung và \(\widehat {CIH} = \widehat {CKD} = 90^\circ \). Suy ra ( g.g) |
|
nên \(\frac{{CI}}{{CK}} = \frac{{CH}}{{CD}}\) hay \[CI.CD = CH.CK\] |
|
Xét \(\Delta OAB\) cân tại \[O\]có đường cao \[OK\]nên \[OK\] đồng thời là phân giác Khi đó \(\widehat {AOK} = \widehat {KOB}\) suy ra cung . Suy ra . |
|
Vậy \[IE\]là phân giác của \[\widehat {AIB}\]nên \(\frac{{HA}}{{HB}} = \frac{{IA}}{{IB}}\) (tính chất đường phân giác) hay \(HA.HB = IA.HB\) |
|
c) Vẽ \(DT\) vuông góc với đường thẳng \(AI\) tại \(T\), đường tròn đường kính \(CK\) cắt đoạn thẳng \(CD\) tại \(G(G \ne D)\). Chứng minh \(K,G,T\) thẳng hàng. |
|
Do vuông tại \[T\]và vuông tại \[K\]nên \({\rm{D}},{\rm{T}},{\rm{A}},{\rm{K}}\) cùng thuộc đường tròn \[DA\]. Khi đó \(\widehat {TKD} = \widehat {TAD}\) (cùng chắn cung TD ) mà \(\widehat {TAD} = \widehat {IAD} = \widehat {IED}\) (cùng chắn cung ID ) nên \(\widehat {TKD} = \widehat {IED}\). Suy ra \[TK\,//\,IE\]. |
|
Do G thuộc đường tròn đường kinh CK nên \(\widehat {CGK} = {90^ \circ }\) nên \(KG \bot CD\) Mà \(EI \bot CD\) (do I thuộc đường tròn đường kính DE ) nên \(KG//EI\) (2) Từ (1) và (2) suy ra \(T,G,K\) thẳng hàng. |
Lời giải
|
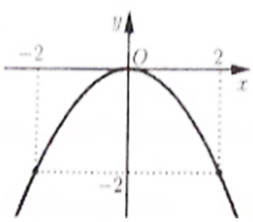
\({\rm{\Delta }} = {(m - 1)^2} - 4\left( { - 3m - 6} \right) = {m^2} - 2m + 1 + 12m + 24 = {(m + 5)^2} \ge 0\) với mọi \(m\). Nên phương trình luôn có hai nghiệm \({x_1},{x_2}\). |
|
Khi đó phương trình có hai nghiệm là: \(x = m + 2\) và \(x = - 3\) |
|
TH1: \({x_1} = m + 2;{x_2} = - 3\) Ta có: \(\left| {{x_1}} \right| = 5 + \left| {{x_2}} \right|\) nên \(\left| {m + 2} \right| = 8\) nên \(m + 2 = 8\) hoặc \(m + 2 = - 8\) suy ra: \(m = 6\) hoặc \(m = - 10\). TH2: \({x_1} = - 3;{x_2} = m + 2\) Ta có: \(3 = 5 + \left| {m + 2} \right|\) nên \(\left| {m + 2} \right| = - 2\) (vô lí) Vậy \(m = 6\) và \(m = - 10\) là các giá trị cần tìm. |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.