Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{y\left( {{x^2} + x} \right) + 2 = {{\left( {{x^4} - {x^2}} \right)}^2}}\\{{x^2} + x - y = 2\sqrt {x + y} }\end{array}} \right.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Điều kiện: \(x + y \ge 0\). Từ phương trình (2) ta có: \({x^2} + x - y = 2\sqrt {x + y} \) biến đổi thành \({x^2} + 2x + 1 = x + y + 2\sqrt {x + y} + 1\) hay \({\left( {x + 1} \right)^2} = {\left( {\sqrt {x + y} + 1} \right)^2}\) Suy ra \(x = \sqrt {x + y} \) hoặc \(\sqrt {x + y} = - x - 2\) |
|
TH 1: \(x = \sqrt {x + y} \) Vì \(x + y \ge 0\) nên \(x \ge 0\). Bình phương 2 vế ta được: \(y = {x^2} - x\) Thay vào phương trình thứ nhất của hệ ta được: \(\left( {{x^4} - {x^2}} \right) + 2 = {\left( {{x^4} - {x^2}} \right)^2}\) \({\left( {{x^4} - {x^2}} \right)^2} - \left( {{x^4} - {x^2}} \right) - 2 = 0\) \(\left( {{x^4} - {x^2} + 1} \right)\left( {{x^4} - {x^2} - 2} \right) = 0\) \({x^4} - {x^2} - 2 = 0\) do \({x^4} - {x^2} + 1 = {\left( {{x^2} - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\) \(\left( {{x^2} + 1} \right)\left( {{x^2} - 2} \right) = 0\) \({x^2} - 2 = 0\) do \({x^2} + 1 \ge 1 > 0\) với mọi \(x \in \mathbb{R}\) \(x = \sqrt 2 \) (do \(x > 0)\) Với \(x = \sqrt 2 \), ta được \(y = 2 - \sqrt 2 \) TH 2: \(\sqrt {x + y} = - x - 2\) Với \( - x - 2 \ge 0\) hay \(x \le - 2\), bình phương hai vế ta được \({\rm{x}} + y = {x^2} + 4x + 4\) hay \(y = {x^2} + 3x + 4\). Thay vào phương trình thứ nhất của hệ ta được: \(\left( {{x^2} + 3x + 4} \right)\left( {{x^2} + x} \right) + 2 = {\left( {{x^4} - {x^2}} \right)^2}\) \({x^4} + 4{x^3} + 7{x^2} + 4x + 2 = {x^8} - 2{x^6} + {x^4}\) \({x^8} - 2{x^6} - 4{x^3} - 7{x^2} - 4x - 2 = 0\) \({x^6}\left( {{x^2} - 2} \right) - 4{x^2}\left( {x + \frac{7}{4}} \right) - 2\left( {2x + 1} \right) = 0\left( {\rm{*}} \right)\) Vì \(x \le - 2\) nên \({x^6}\left( {{x^2} - 2} \right) > 0, - 4{x^2}\left( {x + \frac{7}{4}} \right) > 0, - 2\left( {2x + 1} \right) > 0\) Do đó \(VT\left( {\rm{*}} \right) > 0\) . Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\sqrt 2 ;2 - \sqrt 2 } \right)\) |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
|
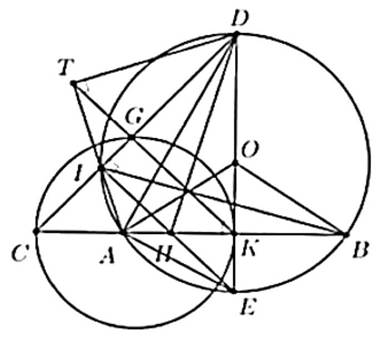
a) Chứng minh tứ giác \(DIHK\) nội tiếp đường tròn. |
|
Ta có có \(\widehat {DIE} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) |
|
\(\Delta \,DKH\) vuông tại\[K\] nên \(D,K,H\) cùng thuộc đường tròn đường kính \[DH\] |
|
\(\Delta \,DIH\) vuông tại \[I\]nên \(D,I,H\) cùng thuộc đường tròn đường kính \[DH\] |
|
Vậy \(D,I,H,K\) cùng thuộc đường tròn đường kính \[DH\]hay tứ giác \[DIHK\]nội tiếp đường tròn.
|
|
b) Chứng minh \(CI.CD = CH.CK\) và \(HA.IB = HB.IA\). |
|
Xét và có \(\widehat {DCK}\) chung và \(\widehat {CIH} = \widehat {CKD} = 90^\circ \). Suy ra ( g.g) |
|
nên \(\frac{{CI}}{{CK}} = \frac{{CH}}{{CD}}\) hay \[CI.CD = CH.CK\] |
|
Xét \(\Delta OAB\) cân tại \[O\]có đường cao \[OK\]nên \[OK\] đồng thời là phân giác Khi đó \(\widehat {AOK} = \widehat {KOB}\) suy ra cung . Suy ra . |
|
Vậy \[IE\]là phân giác của \[\widehat {AIB}\]nên \(\frac{{HA}}{{HB}} = \frac{{IA}}{{IB}}\) (tính chất đường phân giác) hay \(HA.HB = IA.HB\) |
|
c) Vẽ \(DT\) vuông góc với đường thẳng \(AI\) tại \(T\), đường tròn đường kính \(CK\) cắt đoạn thẳng \(CD\) tại \(G(G \ne D)\). Chứng minh \(K,G,T\) thẳng hàng. |
|
Do vuông tại \[T\]và vuông tại \[K\]nên \({\rm{D}},{\rm{T}},{\rm{A}},{\rm{K}}\) cùng thuộc đường tròn \[DA\]. Khi đó \(\widehat {TKD} = \widehat {TAD}\) (cùng chắn cung TD ) mà \(\widehat {TAD} = \widehat {IAD} = \widehat {IED}\) (cùng chắn cung ID ) nên \(\widehat {TKD} = \widehat {IED}\). Suy ra \[TK\,//\,IE\]. |
|
Do G thuộc đường tròn đường kinh CK nên \(\widehat {CGK} = {90^ \circ }\) nên \(KG \bot CD\) Mà \(EI \bot CD\) (do I thuộc đường tròn đường kính DE ) nên \(KG//EI\) (2) Từ (1) và (2) suy ra \(T,G,K\) thẳng hàng. |
Lời giải
|
Vì đồ thị hàm số đi qua \(A\left( { - 2; - 2} \right)\) nên thay \(x = - 2;y = - 2\) vào hàm số ta được: \(\left( {m - 2} \right) \cdot {( - 2)^2} = - 2 \Rightarrow \)\(4\left( {m - 2} \right) = - 2 \Rightarrow \)\(m - 2 = - \frac{1}{2} \Rightarrow \)\(m = \frac{3}{2}\). |
|
\(P = 4 \cdot {\left( {\frac{3}{2}} \right)^2} - 2 \cdot \frac{3}{2} + 5 = 11\). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(40^\circ \).
B. \(50^\circ \).
C. \(45^\circ \).
D. \(100^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập