Đội văn nghệ lớp 9A gồm 3 bạn nam: An, Bình, Công và 2 bạn nữ: Nguyệt, Yến. Cô giáo phụ trách chọn ngẫu nhiên 2 bạn từ 5 bạn đó để hát song ca. Tính xác suất của biến cố : “Hai bạn được chọn có ít nhất một bạn nữ”.

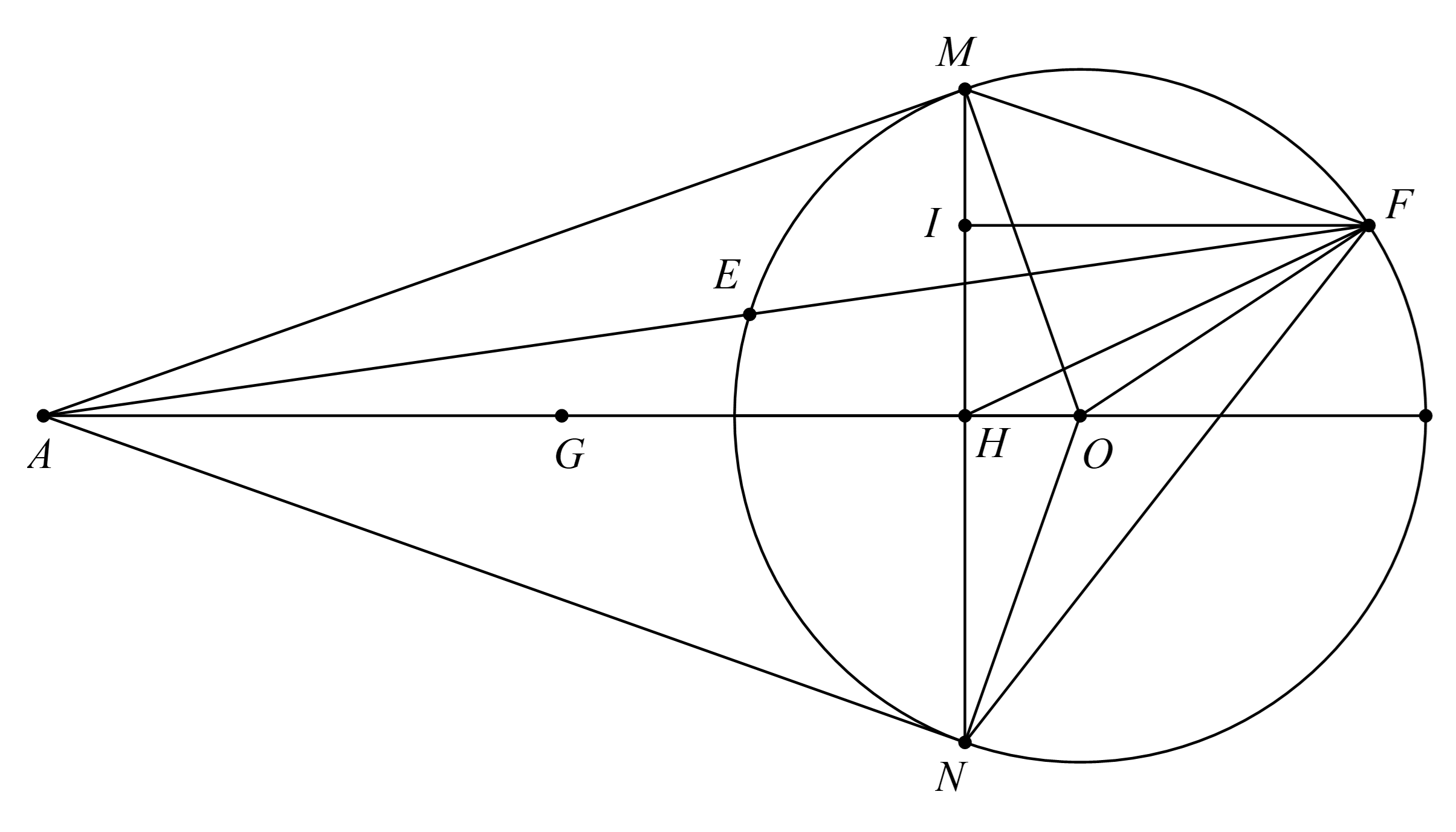
a) Chứng minh tứ giác \(AMON\)là tứ giác nội tiếp.

Gọi \(G\) là trung điểm của \(AO.\)

Xét \(\left( O \right)\) có \(AM\) là tiếp tuyến tại \(M\) (GT) nên \(AM \bot OM\) tại \(M \Rightarrow \widehat {AMO} = 90^\circ \)

Suy ra \(\Delta AMO\) nội tiếp đường tròn tâm \(G\) đường kính \(AO\)

Suy ra \(A,M,O \in \left( {G;\frac{{AO}}{2}} \right)\,\,\left( 1 \right)\)

Xét \((O)\) có \(AN\) là tiếp tuyến tại \(N\) (GT) nên \(AN \bot ON\) tại \(N \Rightarrow \widehat {ANO} = 90^\circ \)

Suy ra  \(\Delta ANO\) nội tiếp đường tròn tâm \(G\) đường kính \(AO\)

Suy ra \(A,N,O \in \left( {G;\frac{{AO}}{2}} \right)\,\,\left( 2 \right)\)

Từ \((1)\) và \((2)\) suy ra \(A,M,N,O \in \left( {G;\frac{{AO}}{2}} \right)\)

Do đó tứ giác\(AMNO\) là tứ giác nội tiếp đường tròn tâm \(G\) đường kính \(AO\).

Vậy tứ giác\(AMNO\) là tứ giác nội tiếp đường tròn tâm \(G\) đường kính \(AO\).

b) Xét tam giác \(AMO\) vuông tại \(M\) có \(AM = \sqrt {O{A^2} - O{M^2}}  = \sqrt {{{\left( {3R} \right)}^2} - {R^2}}  = 2\sqrt 2 R.\)

Theo giả thiết \(AM,\,AN\) là tiếp tuyến của đường tròn \(\left( {O;\,R} \right)\) nên \(AO\) là đường trung trực của \(MN\). Do đó \(AO \bot MN\) tại \(H\).

 Vậy \[AH = \frac{8}{3}R.\]

c) Ta có \(OH = AO - AH = 3R - \frac{{8R}}{3} = \frac{R}{3}.\)

Xét tam giác \(AMH\) vuông tại \(H\) có \(MH = \sqrt {A{M^2} - A{H^2}}  = \sqrt {{{\left( {2\sqrt 2 R} \right)}^2} - {{\left( {\frac{{8R}}{3}} \right)}^2}}  = \frac{{2\sqrt 2 R}}{3}.\)  

Từ đó \(MN = 2MH = \frac{{4\sqrt 2 R}}{3}.\)

Ta có \({S_{\Delta AMN}} = \frac{1}{2}AH.MN = \frac{1}{2}.\frac{{8R}}{3}.\frac{{4\sqrt 2 R}}{3} = \frac{{16\sqrt 2 {R^2}}}{9}.\)

Hạ \(FI \bot MN\) tại \(I.\)ta có:

\({S_{AMFN}} = {S_{\Delta AMN}} + {S_{\Delta FMN}} = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{1}{2}.MN.FI = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{1}{2}.\frac{{4\sqrt 2 R}}{3}.FI\)

\( = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{{2\sqrt 2 R}}{3}.FI\)

Do đó \({S_{AMFN}}\) lớn nhất khi\(FI\) lớn nhất.

Trong tam giác\(FIH\) vuông tại\(I\), ta có:  \(FI \le FH\)

mà \(FH \le OF + OH = R + \frac{R}{3} = \frac{{4R}}{3}\) nên \(FI \le \frac{{4R}}{3}.\)

Từ đó \(FI\) lớn nhất bằng \(\frac{{4R}}{3}\) khi \(d\) đi qua tâm \(O\).

Vậy \({S_{AMFN}}\) đạt giá trị lớn nhất bằng \({S_{AMFN}} = \frac{{16\sqrt 2 {R^2}}}{9} + \frac{{2\sqrt 2 R}}{3}.\frac{{4R}}{3} = \frac{{8\sqrt 2 {R^2}}}{3}\) khi \(d\) đi qua tâm \(O\).

a) Với \(m = 2\) phương trình đã cho trở thành 

\({x^2} - 5x + 6 = 0\).

\(\Delta  = 1 > 0\)

Phương trình đã cho có hai nghiệm phân biệt

\({x_1} = 2\)

\({x_2} = 3\)

Vậy phương trình đã cho có hai nghiệm phân biệt  \({x_1} = 2\), \({x_2} = 3\).

b) \(\Delta  = {\left( {2m + 1} \right)^2} - 4\left( {4m - 2} \right)\)\( = {\left( {2m - 3} \right)^2}\)

Phương trình đã cho có hai nghiệm phân biệt khi \(\Delta  > 0\)

\({\left( {2m - 3} \right)^2} > 0\)

\(2m - 3 \ne 0\)

\(m \ne \frac{3}{2}\).

Với \(m \ne \frac{3}{2}\) phương trình đã cho có hai nghiệm phân biệt \({x_1},\,{x_2}\).

Theo định lý Viète, ta có:

\({x_1} + {x_2} = 2m + 1\)  (1)

\({x_1}{x_2} = 4m - 2\)    (2)

Ta có: \(T = \left( {1 + x_1^2} \right).\left( {1 + x_2^2} \right)\)

\( = x_1^2 + x_2^2 + {\left( {{x_1}{x_2}} \right)^2} + 1\)

\( = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2} + 1\)   (3)

Thay (1) và (2) vào (3) ta được:

\(T = {\left( {2m + 1} \right)^2} - 2\left( {4m - 2} \right) + {\left( {4m - 2} \right)^2} + 1\)

\( = 4{m^2} + 4m + 1 - 8m + 4 + 16{m^2} - 16m + 4 + 1\)

\( = 20{m^2} - 20m + 10\)

\( = 20{\left( {m - \frac{1}{2}} \right)^2} + 5\)

Ta có \({\left( {m - \frac{1}{2}} \right)^2} \ge 0,\forall m\) nên \(T = 20{\left( {m - \frac{1}{2}} \right)^2} + 5 \ge 5,\forall m\)

Dấu "=" xảy ra khi \(m = \frac{1}{2}\) (thỏa mãn)

Vậy giá trị nhỏ nhất của \(T\) bằng \(5\) khi \(m = \frac{1}{2}\).