Cho hàm số \(y = 2{x^2}\) có đồ thị \(\left( P \right)\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số.
b) Tìm các điểm thuộc parabol \(\left( P \right)\) có tung độ bằng 2.
Cho hàm số \(y = 2{x^2}\) có đồ thị \(\left( P \right)\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số.
b) Tìm các điểm thuộc parabol \(\left( P \right)\) có tung độ bằng 2.
Quảng cáo
Trả lời:
a) Ta có bảng giá trị:
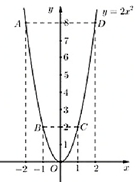
Đồ thị hàm số là đường cong Parabol đi qua các điểm \(O\left( {0;0} \right)\); \[A\left( { - 2;8} \right)\]; \(B\left( { - 1;2} \right)\); \(C\left( {1;2} \right)\); \(D\left( {2;8} \right)\)
Hệ số \(a = 2 > 0\) nên Parabol có bề lõm hướng lên. Đồ thị hàm số nhận \(Oy\)làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:
b) Tìm các điểm thuộc parabol \(\left( P \right)\) có tung độ bằng 2.
Thay \(y = 2\) vào \(y = 2{x^2}\), ta được: \(2 = 2{x^2}\) nên \({x^2} = 1\).
Suy ra \[x = 1{\rm{\;}}\]hoặc\[x = - 1\].
Vậy các điểm thuộc parabol \(\left( {\rm{P}} \right)\) có tung độ bằng 2 là \(\left( {1;2} \right)\); \(\left( { - 1;2} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích đáy của li nước là \(250\;\)\({\rm{c}}{{\rm{m}}^{\rm{2}}}\) nên ta có thể tích nước dâng lên là:
\(V = 0,5.250 = 125\) \(\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\)
Gọi \(x\) \[\left( {{\rm{cm}}} \right)\] là độ dài cạnh của viên xúc xắc, thể tích viên xúc xắc là: \({x^3}\)
Thề tích viên xúc xắc bằng thể tích nước dâng lên, nên ta có:
\({x^3} = 125\) suy ra \(x = \sqrt[3]{{125}} = 5\) \[\left( {{\rm{cm}}} \right)\]
Vậy cạnh của con xúc xắc bằng 5 cm .
Lời giải
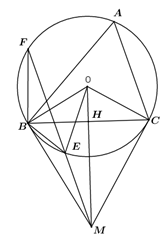
Ta có \(MB = MC\) (tính chất hai tiếp tuyến cắt nhau)
\(OB = OC\) (cùng bằng bán kính của \(\left( O \right)\)
Suy ra \[OM\] là trung trực của \[BC\]. Suy ra \(MO \bot BC\) tại H .
Do MB là tiếp tuyến nên \(MB \bot OB\) suy ra \(\widehat {MBO} = \widehat {MHB} = 90^\circ \)
Kết hợp với \(\widehat {BMO}\) chung suy ra (g.g)
Khi đó \(\frac{{MB}}{{MO}} = \frac{{MH}}{{MB}}\) hay \[M{B^2} = MH.MO\] \(\left( 1 \right)\)
Do \(OB = OE\) nên \(\Delta OBE\) cân tại O suy ra \[\widehat {BOE} = 180^\circ - 2\widehat {OBE}\]
Suy ra \(\widehat {BFE} = \frac{1}{2}\widehat {BOE} = \frac{1}{2}\left( {180^\circ - 2\widehat {OBE}} \right) = 90^\circ - \widehat {OBE} = \widehat {MBE}\)
Xét \(\Delta MBE\) và \(\Delta MFB\) có \(\widehat {FMB}\) chung và \(\widehat {MBE} = \widehat {BFM}\) (cmt)
Suy ra (g.g) nên \(\frac{{MB}}{{MF}} = \frac{{ME}}{{MB}}\) hay \(M{B^2} = ME.MF\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(MH.MO = ME.MF\) (đpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
