Trong đợt kiểm tra cuối kỳ II môn toán lớp 9, một phòng kiểm tra của trường có 24 thí sinh dự kiểm tra. Các thí sinh đều phải làm bài trên giấy kiểm tra của trường phát. Cuối buổi kiểm tra, sau khi thu bài, giám thị coi kiểm tra đếm được tổng số tờ là 53 tờ giấy kiểm tra. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy kiểm tra, bao nhiêu thí sinh làm bài 3 tờ giấy kiểm tra? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy kiểm tra.

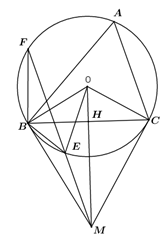
Ta có \(MB = MC\) (tính chất hai tiếp tuyến cắt nhau)

\(OB = OC\) (cùng bằng bán kính của \(\left( O \right)\)

Suy ra \[OM\] là trung trực của \[BC\]. Suy ra \(MO \bot BC\) tại H .

Do MB là tiếp tuyến nên \(MB \bot OB\) suy ra \(\widehat {MBO} = \widehat {MHB} = 90^\circ \)

Kết hợp với \(\widehat {BMO}\) chung suy ra  (g.g)

Khi đó \(\frac{{MB}}{{MO}} = \frac{{MH}}{{MB}}\) hay \[M{B^2} = MH.MO\]       \(\left( 1 \right)\)

Do \(OB = OE\) nên \(\Delta OBE\) cân tại O suy ra \[\widehat {BOE} = 180^\circ  - 2\widehat {OBE}\]

Suy ra \(\widehat {BFE} = \frac{1}{2}\widehat {BOE} = \frac{1}{2}\left( {180^\circ  - 2\widehat {OBE}} \right) = 90^\circ  - \widehat {OBE} = \widehat {MBE}\)

Xét \(\Delta MBE\) và \(\Delta MFB\) có \(\widehat {FMB}\) chung và \(\widehat {MBE} = \widehat {BFM}\) (cmt)

Suy ra  (g.g) nên \(\frac{{MB}}{{MF}} = \frac{{ME}}{{MB}}\) hay \(M{B^2} = ME.MF\)    \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(MH.MO = ME.MF\) (đpcm)

Diện tích đáy của li nước là \(250\;\)\({\rm{c}}{{\rm{m}}^{\rm{2}}}\) nên ta có thể tích nước dâng lên là:

                  \(V = 0,5.250 = 125\) \(\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\)

                     Gọi \(x\) \[\left( {{\rm{cm}}} \right)\] là độ dài cạnh của viên xúc xắc, thể tích viên xúc xắc là: \({x^3}\)

                  Thề tích viên xúc xắc bằng thể tích nước dâng lên, nên ta có:

                  \({x^3} = 125\) suy ra \(x = \sqrt[3]{{125}} = 5\) \[\left( {{\rm{cm}}} \right)\]

                     Vậy cạnh của con xúc xắc bằng 5 cm .