Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Ninh Thuận năm học 2025-2026 có đáp án

Ta có: \(f\left( 1 \right) = 2.1 + 2024 = 2026\).

                 Vậy \(f\left( x \right) = 2026\) khi \(x = 1\)

a) Ta có bảng giá trị:

 Đồ thị hàm số là đường cong Parabol đi qua các điểm \(O\left( {0;0} \right)\); \[A\left( { - 2;8} \right)\]; \(B\left( { - 1;2} \right)\); \(C\left( {1;2} \right)\); \(D\left( {2;8} \right)\)

                 Hệ số \(a = 2 > 0\) nên Parabol có bề lõm hướng lên. Đồ thị hàm số nhận \(Oy\)làm trục đối xứng.

                 Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:

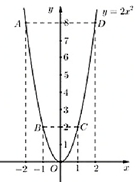
b) Tìm các điểm thuộc parabol \(\left( P \right)\) có tung độ bằng 2.

Thay \(y = 2\) vào \(y = 2{x^2}\), ta được: \(2 = 2{x^2}\)  nên \({x^2} = 1\).

Suy ra \[x = 1{\rm{\;}}\]hoặc\[x =  - 1\].

Vậy các điểm thuộc parabol \(\left( {\rm{P}} \right)\) có tung độ bằng 2 là \(\left( {1;2} \right)\); \(\left( { - 1;2} \right)\).

Xét phương trình \(2{x^2} + 4x - 5 = 0\) có \(\Delta  = {4^2} - 4.2.\left( { - 5} \right) = 56 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1}\); \({x_2}\).

                 Áp dụng định lí Viète, ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} =  - \frac{4}{2} =  - 2}\\{{x_1}{x_2} = \frac{{ - 5}}{2}}\end{array}} \right.\)

                   Ta có:           \(T = \frac{{2{x_1} - 1}}{{{x_2}}} + \frac{{2{x_2} - 1}}{{{x_1}}} + 2026\)

                                        \( = \frac{{{x_1}\left( {2{x_1} - 1} \right)}}{{{x_1}{x_2}}} + \frac{{{x_2}\left( {2{x_2} - 1} \right)}}{{{x_1}{x_2}}} + \frac{{2026{x_1}{x_2}}}{{{x_1}{x_2}}}\)

                                        \( = \frac{{2x_1^2 - {x_1} + 2x_2^2 - {x_2} + 2026{x_1}{x_2}}}{{{x_1}{x_2}}}\)

                                        \( = \frac{{\left( {2x_1^2 + 4{x_1}{x_2} + 2x_2^2} \right) - \left( {{x_1} + {x_2}} \right) + 2022{x_1}{x_2}}}{{{x_1}{x_2}}}\)

                                        \( = \frac{{2{{\left( {{x_1} + {x_2}} \right)}^2} - \left( {{x_1} + {x_2}} \right) + 2022{x_1}{x_2}}}{{{x_1}{x_2}}}\)

                                        \( = \frac{{2 \cdot {{( - 2)}^2} - \left( { - 2} \right) + 2022 \cdot \left( {\frac{{ - 5}}{2}} \right)}}{{\frac{{ - 5}}{2}}}\)

                                        \( = \frac{{8 + 2 - 5055}}{{\frac{{ - 5}}{2}}} = 2018\)

                     Vậy \(T = 2018\)

Gọi \(x,y\) lần lượt là số thí sinh làm 2 tờ giấy và 3 tờ giấy kiểm tra (tờ) \(\left( {0 < x,y < 21} \right)\)

                  Phòng kiểm tra của trường có 24 thí sinh dự kiểm tra nên ta có: \(x + y + 3 = 24\)

                     Cuối buổi kiểm tra, sau khi thu bài, giám thị coi kiểm tra đếm được tổng số tờ là 53 tờ giấy kiểm tra nên ta có: \(2x + 3y + 3 = 53\)

                     Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y + 3 = 24}\\{2x + 3y + 3 = 53}\end{array}} \right.\)

                     \(\left\{ {\begin{array}{*{20}{l}}{x + y = 21}\\{2x + 3y = 50}\end{array}} \right.\)

                      \(\left\{ {\begin{array}{*{20}{l}}{x = 13}\\{y = 8}\end{array}} \right.\) (thỏa mãn điều kiện)

                  Vậy có 13 học sinh làm 2 tờ giấy kiểm tra, 8 học sinh làm 3 tờ giấy kiểm tra.

a) Không gian mẫu của phép thử là:\[\Omega  = \left\{ {\left( {1;2} \right),\left( {1;3} \right),\left( {1;4} \right),\left( {1;5} \right),\left( {1;6} \right),\left( {2;3} \right),\left( {2;4} \right),\left( {2;5} \right),\left( {2;6} \right),\left( {3;4} \right),\left( {3;5} \right),\left( {3;6} \right),\left( {4;5} \right),\left( {4;6} \right),\left( {5;6} \right)} \right\}\]

                 b) Tính xác suất để lấy được hai quả đều có số chã̃n.

                 Không gian mẫu có 15 phần tử.

                 Các kết quả thuận lợi cho biến cố lấy được hai quả đều có số chẵn là: \(\left( {2;4} \right),\left( {2;6} \right),\left( {4;6} \right)\).

                 Có 3 kết quả thuận lợi.

                 Xác suất đề lấy được hai quả đều có số chẵn là: \(\frac{3}{{15}} = \frac{1}{5}\).

                 Vậy xác suất để lấy được hai quả đều có số chẵn là \(\frac{1}{5}\).