Một hộp đựng 6 quả bóng bàn cân đối đồng chất, được đánh số từ 1 đến 6. Lấy ngẫu nhiên cùng lúc 2 quả:

                  a) Xác định không gian mẫu của phép thử?

                  b) Tính xác suất để lấy được hai quả đều có số chẵn.

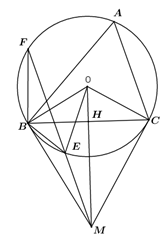
Ta có \(MB = MC\) (tính chất hai tiếp tuyến cắt nhau)

\(OB = OC\) (cùng bằng bán kính của \(\left( O \right)\)

Suy ra \[OM\] là trung trực của \[BC\]. Suy ra \(MO \bot BC\) tại H .

Do MB là tiếp tuyến nên \(MB \bot OB\) suy ra \(\widehat {MBO} = \widehat {MHB} = 90^\circ \)

Kết hợp với \(\widehat {BMO}\) chung suy ra  (g.g)

Khi đó \(\frac{{MB}}{{MO}} = \frac{{MH}}{{MB}}\) hay \[M{B^2} = MH.MO\]       \(\left( 1 \right)\)

Do \(OB = OE\) nên \(\Delta OBE\) cân tại O suy ra \[\widehat {BOE} = 180^\circ  - 2\widehat {OBE}\]

Suy ra \(\widehat {BFE} = \frac{1}{2}\widehat {BOE} = \frac{1}{2}\left( {180^\circ  - 2\widehat {OBE}} \right) = 90^\circ  - \widehat {OBE} = \widehat {MBE}\)

Xét \(\Delta MBE\) và \(\Delta MFB\) có \(\widehat {FMB}\) chung và \(\widehat {MBE} = \widehat {BFM}\) (cmt)

Suy ra  (g.g) nên \(\frac{{MB}}{{MF}} = \frac{{ME}}{{MB}}\) hay \(M{B^2} = ME.MF\)    \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(MH.MO = ME.MF\) (đpcm)

Diện tích đáy của li nước là \(250\;\)\({\rm{c}}{{\rm{m}}^{\rm{2}}}\) nên ta có thể tích nước dâng lên là:

                  \(V = 0,5.250 = 125\) \(\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\)

                     Gọi \(x\) \[\left( {{\rm{cm}}} \right)\] là độ dài cạnh của viên xúc xắc, thể tích viên xúc xắc là: \({x^3}\)

                  Thề tích viên xúc xắc bằng thể tích nước dâng lên, nên ta có:

                  \({x^3} = 125\) suy ra \(x = \sqrt[3]{{125}} = 5\) \[\left( {{\rm{cm}}} \right)\]

                     Vậy cạnh của con xúc xắc bằng 5 cm .