Cho phương trình \({x^2} - mx - 2 = 0\) (với \[m\] là tham số dương) có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} - 2{x_2} = 5\). Biết rằng \[m\] có dạng \(\frac{a}{b}\) là phân số tối giản với mẫu số dương, hiệu \({a^2} - {b^2}\) bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Xét phương trình \({x^2} - mx - 2 = 0\).
Phương trình trên có \(\Delta = {\left( { - m} \right)^2} - 4 \cdot 1 \cdot \left( { - 2} \right) = {m^2} + 8 > 0\) với mọi tham số \[m.\]
Do đó phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\).
Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\,\,\,\,\left( 1 \right)\\{x_1}{x_2} = - 2\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right..\)
Theo bài, ta có \({x_1} - 2{x_2} = 5\) suy ra \[{x_1} = 2{x_2} + 5,\] thay vào \(\left( 1 \right),\) ta được:
\(2{x_2} + 5 + {x_2} = m\) hay \(3{x_2} = m - 5\) nên \({x_2} = \frac{{m - 5}}{3}.\)
Khi đó, ta có \[{x_1} = 2 \cdot \frac{{m - 5}}{3} + 5 = \frac{{2m + 5}}{3}.\]
Thay \[{x_1} = \frac{{2m + 5}}{3}\] và \({x_2} = \frac{{m - 5}}{3}\) vào \(\left( 2 \right),\) ta được:
\[\frac{{2m + 5}}{3} \cdot \frac{{m - 5}}{3} = - 2\]
\(2{m^2} - 10m + 5m - 25 = - 18\)
\(2{m^2} - 5m - 7 = 0\)
\(m = - 1\) hoặc \(m = \frac{7}{2}.\)
Theo bài, \[m\] có dạng \(\frac{a}{b}\) là phân số tối giản với mẫu số dương nên ta chọn \(m = \frac{7}{2}.\)
Khi đó \(a = 7,\,\,b = 2.\)
Vậy \({a^2} - {b^2} = {7^2} - {2^2} = 45.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
Đặt các điểm \(A,\,\,B,\,\,C\) và cung \(BmC\) như hình vẽ.
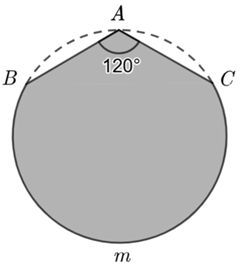
Ta có \(AB = AC = 1,5\,\,{\rm{m}}\) nên \(AB + AC = 2 \cdot 1,5 = 3\,\,\left( {\rm{m}} \right)\).
Vì \(\widehat {BAC}\) nội tiếp chắn nên
Độ dài là: \[\frac{{240^\circ \cdot 2\pi r}}{{360^\circ }} = 2\pi \,\,\left( {\rm{m}} \right).\]
Độ dài đoạn dây đèn dùng trang trí là: \[2\pi \pi + 3 \approx 9,3\,\,\left( {\rm{m}} \right)\].
Câu 2
A. 976 cm3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
Thể tích viên gạch dạng hình hộp chữ nhật khi chưa đục lỗ là: \(8 \cdot 8 \cdot 22 = 1\,\,408\) (cm3).
Thể tích một lỗ dạng hình trụ là: \(\pi \cdot {\left( {\frac{{2,5}}{2}} \right)^2} \cdot 22 = 34,375\pi \) (cm3).
Thể tích đất sét dùng để làm một viên gạch khi đã đục bốn lỗ là:
\(1\,\,408 - 4 \cdot 34,375\pi = 1\,\,408 - 137,5\pi \approx 976\) (cm3).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập