Một cốc nước hình trụ có bán kính đáy phía trong thành cốc là \[4\,{\rm{cm}}\]đang chứa nước nhưng chưa đầy. Người ta thả chìm hoàn toàn vào cốc \[3\] viên bi hình cầu giống hệt nhau thì thấy mực nước trong cốc dâng lên nhưng chưa đầy cốc. Biết bán kính mỗi viên bi bằng \[2\,{\rm{cm}}\].
a) Tính thể tích của mổi viên bi.
b) Sau khi thả chìm hoàn toàn vào cốc \[3\] viên bi thì thấy chiều cao của mực nước trong cốc dâng lên so với mực nước ban đầu là \(h\,\,{\rm{(cm}}).\) Tính \(h\).

PT đã cho có hai nghiệm phân biệt \({x_1},{x_2}\). Theo định lý Viét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 5}\\{{x_1} \cdot {x_2} = 2}\end{array}} \right.\)

Vì \[{x_1} + {x_2} = 5 > 0,{x_1}.{x_2} = 2 > 0\] nên \[{x_1},{x_2}\] là hai nghiệm dương phân biệt.
Vì \({x_2}\) là nghiệm của PT \({x^2} - 5x + 2 = 0\) nên \({x_2}{\;^2} - 5{x_2} + 2 = 0\) ha\(x_2^2 = 5{x_2} - 2\)

Ta có: \(A = \sqrt {16x_1^2 + 8{x_1}{x_2} + 5{x_2} - 2}  + 3{x_2}\)

\(A = \sqrt {16x_1^2 + 8{x_1}{x_2} + x_2^2}  + 3{x_2}\) \( = \sqrt {{{\left( {4{x_1} + {x_2}} \right)}^2}}  + 3{x_2}\) \( = \left| {4{x_1} + {x_2}} \right| + 3{x_2}\)

Vì \({x_1},{x_2}\) là hai nghiệm dương nên \(A = \left| {4{x_1} + {x_2}} \right| + 3{x_2} = 4\left( {{x_1} + {x_2}} \right) = 4.5 = 20\).

Vậy \(A = 20\).

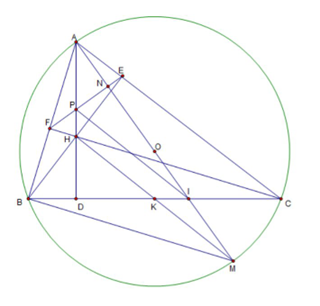
a) \(\widehat {CEH} = 90^\circ \) (vì \(BE\) là đường cao \(\Delta ABC\)) suy ra \(E\) thuộc đường tròn đường kính \(CH\) hay \(E,H,C\) thuộc đường tròn đường kính \(CH\).
\(\widehat {CDH} = 90^\circ \) (vì \(AD\) là đường cao \(\Delta ABC\)) suy ra \(D\) thuộc đường tròn đường kính \(CH\) hay \(D,H,C\) thuộc đường tròn đường kính CH. Vậy \[4\] điểm \(C,E,H,D\) cùng thuộc đường tròn đường kính \(CH\)
b) Xét \(\Delta ADB\) và \(\Delta ACM\).

Ta có \(\widehat {ACM} = 90^\circ \) (góc nội tiếp chắn nửa dường tròn).
\(\widehat {ADB} = 90^\circ \) (vì \(AD\) là đường cao \(\Delta ABC\) ). Suy ra \(\widehat {ADB} = \widehat {ACM} = {90^{\rm{o}}}\) (1)
\(\widehat {ABC} = \widehat {AMC}\) (2 góc nội tiếp cùng chắn cung \(AC\) của \(\left( O \right)\) ) (2)
Từ (1) và (2) suy ra .

Ta có \(\frac{{AD}}{{AC}} = \frac{{BD}}{{MC}}\) suy ra \(AD \cdot MC = BD \cdot AC\)

c) Ta có \(CM\,{\rm{//}}\,BH\) (vì \({\rm{CM}},{\rm{BH}}\) cùng vuông góc với AC ).

\(BM//CH\) (vì \[BM,CH\] cùng vuông góc với \[AB\] ).

Suy ra tứ giác \(BHCM\) là hình bình hành. Khi đó hai đường chéo \(HK\) và \(BC\) cắt nhau tại trung điểm mỗi đường.
\( \Rightarrow K\) là trung điểm của \(HM\).
Ta có .

Ta có tứ giác \(AEHF\) nội tiếp đường tròn đường kính \(AH\)
\( \Rightarrow \widehat {AHF} = \widehat {AEF}\) (góc nội tiếp cùng chắn cung AF) \( \Rightarrow \widehat {AEF} = \widehat {ABI}\).

Từ chứng minh phần b ta có
Xét \(\Delta APE\) và \(\Delta AIB\) có \(\widehat {ABI} = \widehat {AEF};\widehat {EAP} = \widehat {BAI}\)

Tương tự .

Vậy \(PI\,{\rm{//}}\,HK\).