Cho Parabol (P): \(y = {x^2}\) và đường thẳng d: y = ax + b.
a) Vẽ Parabol (P): \(y = {x^2}\) trên mặt phẳng tọa độ Oxy.
b) Tìm a, b để đường thẳng d đi qua điểm A(2; 8) và song song với đường thẳng
d': y = 3x + 2025
c) Với a, b tìm được ở ý b) đường thẳng d cắt Parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\). Hãy tính giá trị của biểu thức \(A = {x_1}^2 + {x_2}^2 - 5{x_1}{x_2}\)
Cho Parabol (P): \(y = {x^2}\) và đường thẳng d: y = ax + b.
a) Vẽ Parabol (P): \(y = {x^2}\) trên mặt phẳng tọa độ Oxy.
b) Tìm a, b để đường thẳng d đi qua điểm A(2; 8) và song song với đường thẳng
d': y = 3x + 2025
c) Với a, b tìm được ở ý b) đường thẳng d cắt Parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\). Hãy tính giá trị của biểu thức \(A = {x_1}^2 + {x_2}^2 - 5{x_1}{x_2}\)
Quảng cáo
Trả lời:
Ta có bảng giá trị sau:
|
x |
\[ - 2\] |
\[ - 1\] |
0 |
1 |
2 |
|
\(y = {x^2}\) |
4 |
1 |
0 |
1 |
4 |
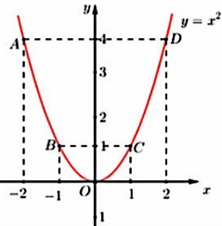
a) Đồ thị hàm số là đường cong parabol đi qua các điểm O(0; 0); A(\[ - 2\];4); B(\[ - 1\];1); C(1;1); D(2;4).
Hệ số a = 1 > 0 nên parabol có bề cong hướng lên.
Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:
b) Vì đường thẳng d song song với đường thẳng d’ nên a = 3; b = 2025.
Ta được đường thẳng d: y = 3x + b.
Vì đường thẳng d đi qua điểm A(2; 8) nên 8 = 3.2 + b, suy ra b = 8 – 3.2 = 2 (TMĐK).
Đường thẳng d là: y = 3x + 2.
Vậy a = 3; b = 2.
c) Đường thẳng d: y = 3x + 2 cắt Parabol (P): \(y = {x^2}\) thì ta có phương trình: \({x^2} = 3x + 2\).
Suy ra \({x^2} - 3x - 2 = 0\)
Vì \(\Delta = {( - 3)^2} - 4.( - 2) = 17 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{{ - 3}}{1} = 3\\{x_1}{x_2} = \frac{{ - 2}}{1} = - 2\end{array} \right.\).
Ta có: \(A = {x_1}^2 + {x_2}^2 - 5{x_1}{x_2} = {({x_1} + {x_2})^2} - 7{x_1}{x_2} = {3^2} - 7.( - 2) = 23\).
Vậy A = 23.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
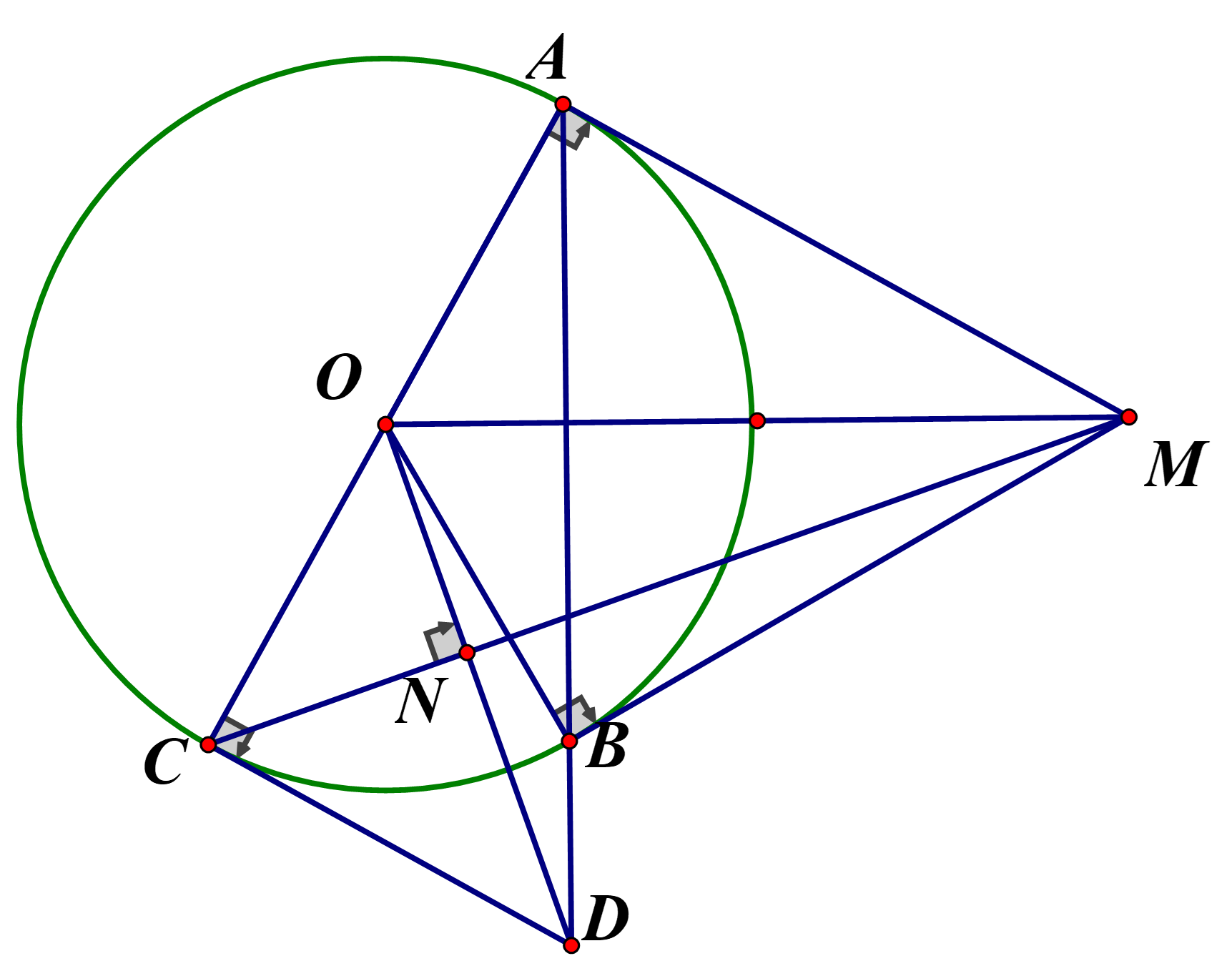
a) Do MA, MB là tiếp tuyến của (O) nên MA \( \bot \) OA, MB \( \bot \) OB
Khi đó \(\Delta \)MAO vuông tại A nên M, A, O cùng thuộc đường tròn đường kính OM
\(\Delta \)MBO vuông tại B nên M, B, O cùng thuộc đường tròn đường kính OM
Vậy M, O, A, B cùng thuộc đường tròn đường kính OM hay tứ giác OAMB nội tiếp.
b) Ta có \(\widehat {ABC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta \)ABC vuông tại B
Khi đó \(\cos \widehat {OCB} = \frac{{BC}}{{AC}} = \frac{4}{{2.3}} = \frac{2}{3}\) suy ra \(\widehat {OCB} \approx 48,2^\circ .\)
c) Gọi H là giao điểm của OM và AB.
Ta có MA = MB (tính chất 2 tiếp tuyến cắt nhau) và OA = OB (cùng là bán kính)
Nên OM là trung trực của AB. Khi đó OM \( \bot \) AB tại trung điểm H của AB
Khi đó (g.g) suy ra \(O{A^2} = OH.OM\)
Mà OA = OC nên \(O{C^2} = OH.OM\) suy ra \(\frac{{OH}}{{OC}} = \frac{{OC}}{{OM}}\)
Kết hợp \(\widehat {COM}\) chung nên (c.g.c)
Suy ra \(\widehat {OHC} = \widehat {OCM}\) (hai góc tương ứng).
Do \(\Delta \)OHD vuông tại H và \(\Delta \)OCD vuông tại C nên O, H, C, D cùng thuộc đường tròn đường kính OD
Suy ra \(\widehat {OHC} = \widehat {ODC}\). Suy ra \(\widehat {OCM} = \widehat {ODC}\)
Mà \(\widehat {OCM} + \widehat {MCD} = 90^\circ \) nên \(\widehat {ODC} + \widehat {MCD} = {90^ \circ }\) hay \(\Delta \)CDN vuông tại N
Xét \(\Delta \)CDN và \(\Delta \)MCA có \(\widehat {DNC} = \widehat {MAC} = 90^\circ ,\,\,\widehat {ODC} = \widehat {OCM}.\)
Suy ra (g.g) (đpcm).
Lời giải
Gọi x (km/h) là vận tốc trung bình của bạn Bình (x > 0)
Khi đó vận tốc trung bình của An là: x + 5 (km/h)
Thời gian đi của Bình là: \(\frac{{10}}{x}\) (h)
Thời gian đi của An là: \(\frac{{10}}{{x + 5}}(h)\)
Do An đến B trước Bình 6 phút = \(\frac{1}{{10}}(h)\) nên ta có:
\(\begin{array}{l}\frac{{10}}{x} - \frac{{10}}{{x + 5}} = \frac{1}{{10}}\\\frac{{10(x + 5)}}{{x(x + 5)}} - \frac{{10x}}{{x(x + 5)}} = \frac{1}{{10}}\\\frac{{50}}{{x(x + 5)}} = \frac{1}{{10}}\\500 = x(x + 5)\\{x^2} + 5x - 500 = 0\end{array}\)
Giải phương trình ta được x = 20 (TM); x = −25 (loại)
Vậy vận tốc của Bình là 20 km/h, vận tốc của An là 25 km/h.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
