Câu hỏi:
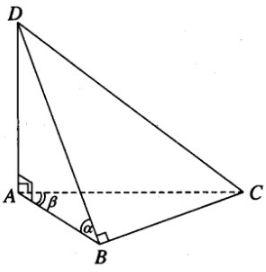
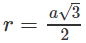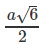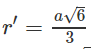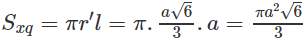24/06/2020 10,379Cho tứ diện ABCD có AD (ABC) và BD BC. Khi quay tất cả các cạnh của tứ diện đó quanh cạnh AB có những hình nón nào được tạo thành ? Hãy kể tên các hình nón đó.
Câu hỏi trong đề: Giải SBT Toán 12 Đề toán tổng hợp chương 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tứ diện ABCD có BAD = 90 nên ABD = là một góc nhọn. Khi quay các cạnh của tứ diện đó xung quanh cạnh AB thì cạnh BD tạo thành một hình nón tròn xoay đỉnh B có trục là AB, cạnh AD vuông góc với AB tạo thành đáy của hình nón đó.
Mặt khác theo giả thiết ta có BD BC nên AB BC. Ta có BAC = là một góc nhọn. Do đó khi quay các cạnh của tứ diện xung quanh cạnh AB thì cạnh AC tạo thành một hình nón tròn xoay đỉnh A có trục là AB, còn cạnh BC tạo thành đáy của hình nón.
Như vậy khi quay tất cả các cạnh của tứ diện xung quanh trục AB thì các cạnh BD và AC tạo thành hai hình nón.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
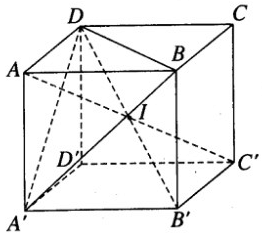
Gọi I là tâm của hình lập phương. Tất cả các đỉnh của hình lập phương đều có khoảng cách đến I bằng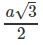 
nên chúng nằm trên mặt cầu tâm I bán kính 
Ta có diện tích mặt cầu đó là
Lời giải
Đường tròn đáy của hình nón tròn xoay đỉnh A tạo nên bởi cạnh AB là đường tròn ngoại tiếp tam giác đều A’BD, tam giác này có cạnh bằng a và có đường cao bằng 
Do đó đường tròn đáy hình nón có bán kính 
Vậy hình nón tròn xoay này có đường sinh l = a và có diện tích xung quanh là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)