Câu hỏi:
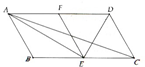
13/07/2024 14,501Cho hình bình hành ABCD có BC = 2AB và Gọi E, F lần lượt là trung điểm của BC và AD.
a) Chứng minh tứ giác ECDF là hình thoi.
b) Tứ giác ABED là hình gì ?
c) Tính số đo của góc
Câu hỏi trong đề: Ôn tập chương I và kiểm tra đánh giá !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta sẽ có FD//EC và FD = EC = 0.5 AD Þ ECDF là hình bình hành.
Mà
Þ AB = BE = EF = EC
Þ CDFE là hình thoi.
b) Tứ giác ABED là hình thang cân vì BE//AD và
c) Ta có , F là trung điểm AD Þ
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) DDAE = DBAF (c.g.c)
và AE = AF
Mà
Þ DAEF vuông cân tại A.
b) DEAF vuông cân nên IA = IE = FI (1); DCFE vuông có IC là đường trung tuyến Þ IE = IC = IF (2);
Từ (1) và (2) suy ra Þ IA = IC nên I thuộc trung trực của AC hay I thuộc BD.
c) Do K đối xứng với A qua I nên I là trung điểm của AK.
Mà I là trung điểm của EF(gt) nên AFKE là hình bình hành, DAEF vuông cân tại A nên AI ^ EF.
Vậy AFKE là hình vuông.
Lời giải
a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.
Þ = 450 Þ DACE vuông cân.
b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.
c) Do AH ^ BN, mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.
d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ = 900
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4