Cho hình trụ có diện tích xung quanh bằng 50$\mathrm{\pi }$ và độ dài đường sinh bằng đường kính của đường tròn đáy. Tính bán kính r của đường tròn đáy.

Đáp án D

Đáp án C

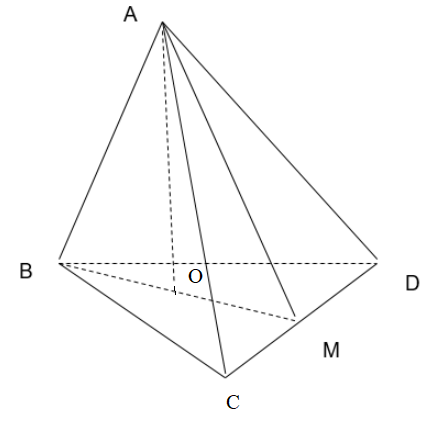
Gọi M là trung điểm của CD, \(\alpha \)là góc BAM.

Có \(CD \bot AM,CD \bot BM \Rightarrow CD \bot \left( {ABM} \right)\)

Kẻ \(AO \bot BM\)

\( \Rightarrow AO \bot CD\)

\( \Rightarrow AO \bot \left( {BCD} \right)\)

Xét \(\Delta BAM\), có:

\(cos\alpha  = \frac{x}{6} \Rightarrow \sin \alpha  = \sqrt {1 - \frac{{{x^2}}}{{36}}} \)

\( \Rightarrow OA = AB.\sin \alpha  = x.\sqrt {1 - \frac{{{x^2}}}{{36}}} \)

Khi đó thể tích khối chóp ABCD là: \({V_{ABCD}} = \frac{1}{3}.\frac{{{{\left( {2\sqrt 3 } \right)}^2}\sqrt 3 }}{4}x.\sqrt {1 - \frac{{{x^2}}}{{36}}}  = 6\sqrt 3 .\frac{x}{6}.\sqrt {1 - \frac{{{x^2}}}{{36}}} \)

Áp dụng BĐT Cosi, ta có: \(\frac{x}{6}.\sqrt {1 - \frac{{{x^2}}}{{36}}}  \le \frac{{\frac{{{x^2}}}{{36}} + 1 - \frac{{{x^2}}}{{36}}}}{2} = \frac{1}{2}\)

Do đó thể tích hình chóp lớn nhất là: \(3\sqrt 3 \)

Dấu “=” xảy ra khi \(\frac{x}{6} = \sqrt {1 - \frac{{{x^2}}}{{36}}} \)

\( \Leftrightarrow \frac{{{x^2}}}{{36}} = 1 - \frac{{{x^2}}}{{36}}\)

\( \Leftrightarrow {x^2} = 18\)

\( \Leftrightarrow x = 3\sqrt 2 \)

Vậy với \(x = 3\sqrt 2 \) thì thể tích khối chóp lớn nhất.