Cho tam giác ABC vuông tại A có $\hat{A B C} = α$ (Hình 2).

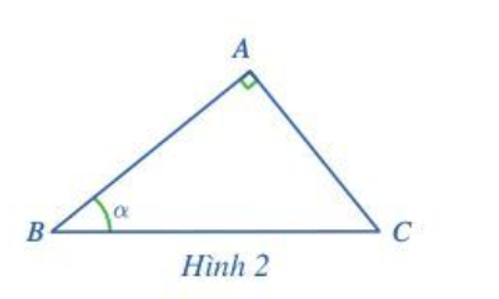
a) Nhắc lại định nghĩa sin α, cos α, tan α, cot α.

b) Biểu diễn tỉ số lượng giác của góc 90° – α theo tỉ số lượng giác của góc α.

Câu hỏi trong đề: Bài tập Giá trị lượng giá của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Tam giác ABC vuông tại A có $\hat{A B C} = α$ . Khi đó ta có:

$\sin α = \frac{A C}{B C}, \cos α = \frac{A B}{B C}, \tan α = \frac{A C}{A B}, \cot α = \frac{A B}{A C}$ .

b) Áp dụng công thức tỉ số lượng giác của 2 góc phụ nhau, ta có:

sin(90° – α) = cos α;

cos(90° – α) = sin α;

tan(90° – α) = cot α;

cot(90° – α) = tan α.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hướng tạo với nhau góc 75°. Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?

Xem đáp án

Lời giải

Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ nên sau 2,5 giờ thì tàu thứ nhất chạy được 8 . 2,5 = 20 (hải lí).

Tàu thứ hai chạy với tốc độ 12 hải lí một giờ nên sau 2,5 giờ thì tàu thứ hai chạy được 12 . 2,5 = 30 (hải lí).

Hai tàu cùng chạy từ bến A và đi thẳng về 2 vùng biển khác nhau theo hướng tạo với nhau góc 75°, giả sử tàu thứ nhất chạy về vùng biển B và tàu thứ hai chạy về vùng biển C, ta có hình vẽ mô phỏng như sau:

Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hướng tạo với nhau góc 75° (ảnh 1)

Khi đó khoảng cách giữa hai tàu sau 2,5 giờ chính là khoảng cách giữa B và C.

Áp dụng định lí côsin trong tam giác ABC ta có:

BC² = AB² + AC² – 2AB. AC. cos A = 20² + 30² – 2 . 20 . 30 . cos 75° ≈ 989,4

Suy ra: BC ≈ 31,5 (hải lí).

Vậy sau 2,5 giờ thì khoảng cách giữa hai tàu là 31,5 hải lí.

Câu 2

Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là α = 35°; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là β = 75°; khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?

Xem đáp án

Lời giải

Ta đặt tên các điểm như trên hình vẽ dưới:

Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A (ảnh 2)

Ta có: AI là khoảng cách từ đỉnh của tòa nhà tới mắt bạn A nên AI = 1,5 m.

BE là khoảng cách từ mặt đất tới mắt của bạn B nên BE = 1,5 m.

Lại có: h = IB + BE ⇒ IB = h – BE = 20 – 1,5 = 18,5 (m).

Và AB = AI + IB = 1,5 + 18,5 = 20 (m).

Ta có: $\hat{C A B} = α + 90 ° = 35 ° + 90 ° = 125 °$ ; $\hat{A B C} = 90 ° - β = 90 ° - 75 ° = 15 °$

Tam giác ABC có $\hat{A B C} + \hat{C A B} + \hat{A C B} = 180 °$ (định lí tổng ba góc trong tam giác)

Suy ra $\hat{A C B} = 180 ° - (\hat{A B C} + \hat{C A B}) = 180 ° - (15 ° + 125 °) = 40 °$

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{A B}{\sin \hat{A C B}} = \frac{B C}{\sin \hat{C A B}}$

Do đó: $B C = \frac{A B . \sin \hat{C A B}}{\sin \hat{A C B}} = \frac{20. \sin 125 °}{\sin 40 °} \approx 25,5$ .

Tam giác CBH vuông tại H nên $\sin \hat{C B H} = \frac{C H}{B C}$

⇒ CH = BC . sin β = 25,5 . sin 75° ≈ 24,6.

Lại có HK = BE = 1,5 m.

Do đó CK = CH + HK = 24,6 + 1,5 = 26,1 (m).

Vậy chiếc diều bay cao 26,1 m so với mặt đất.

Câu 3