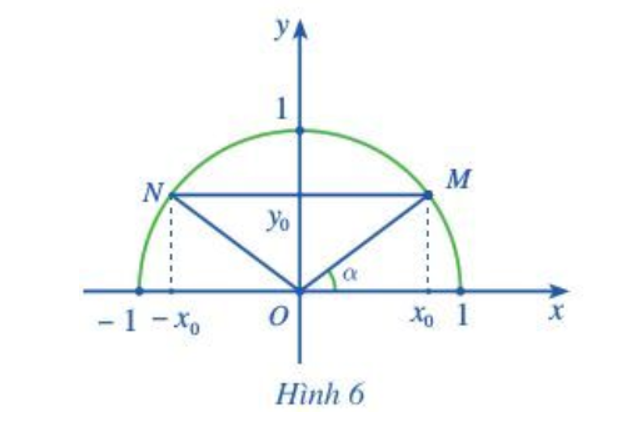
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và (Hình 6).
a) Chứng minh
b) Biểu diễn giá trị lượng giác của góc 180° – α theo giá trị lượng giác của góc α.
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và (Hình 6).
a) Chứng minh
b) Biểu diễn giá trị lượng giác của góc 180° – α theo giá trị lượng giác của góc α.
Quảng cáo
Trả lời:
a) Do MN // Ox nên (hai góc so le trong).
Tam giác OMN có OM = ON (bán kính) nên tam giác OMN cân tại O.
Suy ra .
Ta lại có:
Vậy
b) Do điểm M có tọa độ (x0; y0) thuộc nửa đường tròn đơn vị sao cho nên theo định nghĩa tỉ số lượng giác của góc có giá trị từ 0° đến 180° ta có:
sin α = y0; cos α = x0; ; (1).
Do điểm N có tọa độ (– x0; y0) thuộc nửa đường tròn đơn vị sao cho nên theo định nghĩa tỉ số lượng giác của góc có giá trị từ 0° đến 180° ta có:
sin(180° – α) = y0; cos(180° – α) = – x0;; (2).
Từ (1) và (2) ta có: sin(180° – α) = sin α;
cos(180° – α) = – cos α;
tan(180° – α) = – tan α;
cot(180° – α) = – cot α.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta đặt tên các điểm như trên hình vẽ dưới:
Ta có: AI là khoảng cách từ đỉnh của tòa nhà tới mắt bạn A nên AI = 1,5 m.
BE là khoảng cách từ mặt đất tới mắt của bạn B nên BE = 1,5 m.
Lại có: h = IB + BE ⇒ IB = h – BE = 20 – 1,5 = 18,5 (m).
Và AB = AI + IB = 1,5 + 18,5 = 20 (m).
Ta có: ;
Tam giác ABC có (định lí tổng ba góc trong tam giác)
Suy ra
Áp dụng định lí sin trong tam giác ABC ta có:
Do đó: .
Tam giác CBH vuông tại H nên
⇒ CH = BC . sin β = 25,5 . sin 75° ≈ 24,6.
Lại có HK = BE = 1,5 m.
Do đó CK = CH + HK = 24,6 + 1,5 = 26,1 (m).
Vậy chiếc diều bay cao 26,1 m so với mặt đất.
Lời giải
Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ nên sau 2,5 giờ thì tàu thứ nhất chạy được 8 . 2,5 = 20 (hải lí).
Tàu thứ hai chạy với tốc độ 12 hải lí một giờ nên sau 2,5 giờ thì tàu thứ hai chạy được 12 . 2,5 = 30 (hải lí).
Hai tàu cùng chạy từ bến A và đi thẳng về 2 vùng biển khác nhau theo hướng tạo với nhau góc 75°, giả sử tàu thứ nhất chạy về vùng biển B và tàu thứ hai chạy về vùng biển C, ta có hình vẽ mô phỏng như sau:
Khi đó khoảng cách giữa hai tàu sau 2,5 giờ chính là khoảng cách giữa B và C.
Áp dụng định lí côsin trong tam giác ABC ta có:
BC2 = AB2 + AC2 – 2AB. AC. cos A = 202 + 302 – 2 . 20 . 30 . cos 75° ≈ 989,4
Suy ra: BC ≈ 31,5 (hải lí).
Vậy sau 2,5 giờ thì khoảng cách giữa hai tàu là 31,5 hải lí.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.