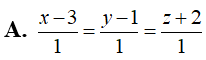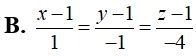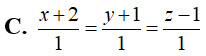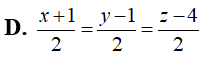Trong không gian Oxyz, cho tam giác ABC với A(1;2;5), B(3;4;1), C(2;3;-3). Gọi G là trọng tâm tam giác ABC và M là điểm thay đổi trên (Oxz). Độ dài GM ngắn nhất bằng
A. 2
B. 3
C. 4
D. 1
Quảng cáo
Trả lời:
Chọn B
Do G là trọng tâm tam giác ABC => G(2;3;1).
Gọi H là hình chiếu vuông góc của G trên mặt phẳng (Oxz), khi đó GH là khoảng cách từ G đến mặt phẳng (Oxz), ta có:
![]()
Với M là điểm thay đổi trên mặt phẳng (Oxz)
![]()
do đó GM ngắn nhất
Vậy độ dài GM ngắn nhất bằng 3
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn B
Cách 1:
![]()
Gọi M,N lần lượt là trung điểm AB, BC
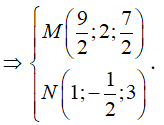
Gọi là véc tơ pháp tuyến của mặt phẳng (ABC).
![]()
![]()
I là tâm đường tròn ngoại tiếp tam giác ABC
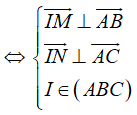
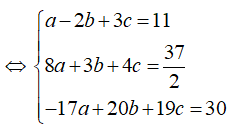
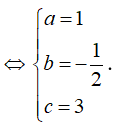
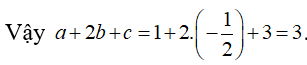
Cách 2:
Ta có
![]()
![]()
=> Tam giác ABC vuông tại B
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên I là trung điểm của AC.
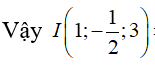
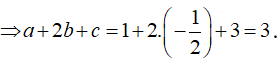
Câu 2
A. T = - 3
B. T = 1
C. T = 3
D. T = - 1
Lời giải
Chọn A
Cách 1: Ta có
![]()
Do ABCD là hình thang cân nên
![]()
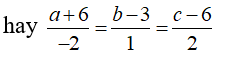
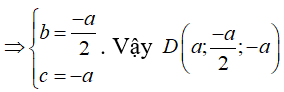
Lại có AC = BD
![]()
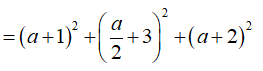
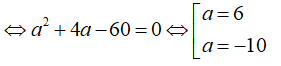
Với a = -10 => D(-10;5;10). Kiểm tra thấy: (Không thỏa mãn ABCD là hình thang cân).
Với a= 6 => D(6; -3; -6). Kiểm tra thấy: 3. ( thỏa mãn).
Do đó
![]()
Cách 2
Ta có
![]()
Do ABCD là hình thang cân nên ngược hướng hay
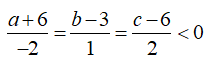
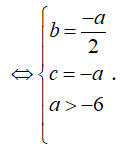
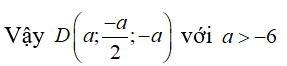
Lại có AB = CD
![]()
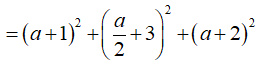
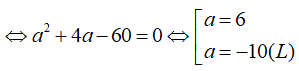
![]()
Do đó
![]()
Cách 3
+ Viết phương trình mặt phẳng trung trực của đoạn thẳng AB( cũng là mp trung trực của đoạn thẳng CD )
+ Gọi mplà mặt phẳng trung trực của đoạn thẳng AB, suy ra mp đi qua trung điểm I(1;2;0) của đoạn thẳng AB và có một vectơ pháp tuyến là
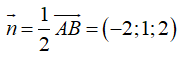
suy ra phương trình của mplà :
![]()
+ Vì C, D đối xứng nhau qua mp nên
![]()
![]()
Công thức trắc nghiệm
Xác định toạ độ điểm là điểm đối xứng của điểm qua mp
![]()
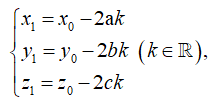
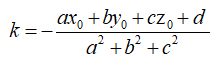
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.