Cho một đa giác đều 48 đỉnh. Lấy ngẫu nhiên 3 đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
Số cách chọn ra 3 đỉnh tùy ý từ 48 đỉnh của đa giác là 
Gọi A là biến cố “tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn”.
* Tính số tam giác tù
+ Chọn đỉnh thứ nhất có 48 cách chọn.
+ Để tạo thành tam giác tù thì ba đỉnh của tam giác phải thuộc cùng nửa đường tròn ngoại tiếp tam giác. Trong đỉnh còn lại sẽ có đỉnh cùng với đỉnh đã chọn thuộc cùng một nửa đường tròn ngoại tiếp. Nên số tam giác tù tạo thành là 48(tam giác).
* Tính số tam giác vuông tạo thành
+ Có 24 đường chéo đi qua tâm đường tròn ngoại tiếp tam giác.
+ Mỗi đường chéo trên cùng với 46 đỉnh còn lại tạ thành 46 tam giác vuông. Nên số tam giác vuông tạo thành là 24.46 = 1104(tam giác).
Do đó:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
Lấy 3 phần tử từ tập S có 
Suy ra số phần tử của không gian mẫu là 
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Đặt 
có 10 phần tử.
có 10 phần tử.
a, b, c là ba số theo thứ tự lập thành cấp số cộng => 2a = b + c
Có 2a là số chẵn, nên b và c cùng chẵn hoặc cùng lẻ.
Suy ra số cách chọn b, c là 
Mỗi cách chọn cặp b, c thì có duy nhất một cách chọn a sao cho 2a = b + c
Suy ra số phần tử của biến cố là 
Xác suất thỏa yêu cầu bài là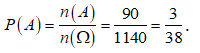 
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A.
Số phần tử của không gian mẫu là n(W =) 6!.
Gọi A là biến cố : "Các bạn học sinh nam ngồi đối diện các bạn nữ".
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
Theo quy tắc nhân ta có cách
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
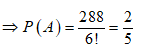
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng , trong đó 1abcd9
A. 0,014
B. 0,0495
C. 0,079
D. 0,055
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập