Câu hỏi:
13/07/2024 4,062
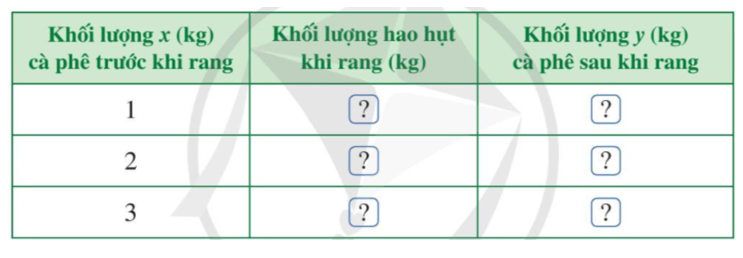
Một doanh nghiệp kinh doanh cà phê cho biết: Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.
a) Tìm số thích hợp cho ở bảng sau:
b) Tìm công thức chỉ mối liên hệ giữa x và y.
c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp đó cần sử dụng bao nhiêu tấn cà phê trước khi rang?
Một doanh nghiệp kinh doanh cà phê cho biết: Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.
a) Tìm số thích hợp cho ở bảng sau:
b) Tìm công thức chỉ mối liên hệ giữa x và y.
c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp đó cần sử dụng bao nhiêu tấn cà phê trước khi rang?
Câu hỏi trong đề: Bài tập cuối chương 6 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.
Khi đó, khối lượng cà phê sau khi rang bằng số phần trăm khối lượng cà phê ban đầu là:
100% - 12% = 88%.
a) Nếu khối lượng cà phê trước khi rang là 1 kg thì:
+ Khối lượng hao hụt khi rang là:
1 . 12% = 0,12 (kg);
+ Khối lượng cà phê sau khi rang là:
1 - 0,12 = 0,88 (kg).
Nếu khối lượng cà phê trước khi rang là 2 kg thì:
+ Khối lượng hao hụt khi rang là:
2 . 12% = 0,24 (kg);
+ Khối lượng cà phê sau khi rang là:
2 - 0,24 = 1,76 (kg).
Nếu khối lượng cà phê trước khi rang là 3 kg thì
+ Khối lượng hao hụt khi rang là:
3 . 12% = 0,36 (kg);
+ Khối lượng cà phê sau khi rang là:
3 - 0,36 = 2,64 (kg).
Ta có bảng sau:
|
Khối lượng x (kg) cà phê trước khi rang |
Khối lượng hao hụt khi rang (kg) |
Khối lượng y (kg) cà phê sau khi rang |
|
1 |
0,12 |
0,88 |
|
2 |
0,24 |
1,76 |
|
3 |
0,36 |
2,64 |
b) Khối lượng cà phê trước và sau khi rang lần lượt là x (kg) và y (kg).
Khối lượng cà phê giảm 12% so với trước khi rang.
Khi đó, khối lượng cà phê sau khi rang bằng 88% khối lượng cà phê trước khi rang nên:
y = 88%x.
Vậy công thức chỉ mối liên hệ giữa x và y là: y = 88%x.
c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp đó cần sử dụng số tấn cà phê trước khi rang là:
2 : 88% = 2 . = ≈ 2,27 (tấn).
Vậy cần khoảng 2,27 tấn cà phê trước khi rang để thu được 2 tấn cà phê sau khi rang.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tính:
a) (x2 + 2x + 3) + (3x2 - 5x + 1);
b) (4x3 - 2x2 - 6) - (x3 - 7x2 + x - 5);
c) -3x2(6x2 - 8x + 1);
d) (4x2 + 2x + 1)(2x - 1);
e) (x6 - 2x4 + x2) : (-2x2);
g) (x5 - x4 - 2x3) : (x2 + x).
Tính:
a) (x2 + 2x + 3) + (3x2 - 5x + 1);
b) (4x3 - 2x2 - 6) - (x3 - 7x2 + x - 5);
c) -3x2(6x2 - 8x + 1);
d) (4x2 + 2x + 1)(2x - 1);
e) (x6 - 2x4 + x2) : (-2x2);
g) (x5 - x4 - 2x3) : (x2 + x).
Xem đáp án »
13/07/2024
9,585
Câu 2:
Cho P(x) = x3 + x2 + x + 1 và Q(x) = x4 - 1. Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).
Cho P(x) = x3 + x2 + x + 1 và Q(x) = x4 - 1. Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).
Xem đáp án »
13/07/2024
6,810
Câu 3:
Cho đa thức P(x) = -9x6 + 4x + 3x5 + 5x + 9x6 - 1.
a) Thu gọn đa thức P(x).
b) Tìm bậc của đa thức P(x).
c) Tính giá trị của đa thức P(x) tại x = -1; x = 0; x = 1.
Cho đa thức P(x) = -9x6 + 4x + 3x5 + 5x + 9x6 - 1.
a) Thu gọn đa thức P(x).
b) Tìm bậc của đa thức P(x).
c) Tính giá trị của đa thức P(x) tại x = -1; x = 0; x = 1.
Xem đáp án »
13/07/2024
5,046
Câu 4:
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) -7x + 5.
b) 2 021x2 - 2 022x + 2 023.
c) 2y3 - + 4.
d) -2tm + 8t2 + t - 1, với m là số tự nhiên lớn hơn 2.
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) -7x + 5.
b) 2 021x2 - 2 022x + 2 023.
c) 2y3 - + 4.
d) -2tm + 8t2 + t - 1, với m là số tự nhiên lớn hơn 2.
Xem đáp án »
13/07/2024
4,554
Câu 5:
Viết đa thức trong mỗi trường hợp sau:
a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6;
b) Đa thức bậc hai có hệ số tự do bằng 4;
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.
Viết đa thức trong mỗi trường hợp sau:
a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6;
b) Đa thức bậc hai có hệ số tự do bằng 4;
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.
Xem đáp án »
13/07/2024
4,546
Câu 6:
Cho hai đa thức: A(x) = 4x4 + 6x2 - 7x3 - 5x - 6 và B(x) = -5x2 + 7x3 + 5x + 4 - 4x4.
a) Tìm đa thức M(x) sao cho M(x) = A(x) + B(x).
b) Tìm đa thức C(x) sao cho A(x) = B(x) + C(x).
Cho hai đa thức: A(x) = 4x4 + 6x2 - 7x3 - 5x - 6 và B(x) = -5x2 + 7x3 + 5x + 4 - 4x4.
a) Tìm đa thức M(x) sao cho M(x) = A(x) + B(x).
b) Tìm đa thức C(x) sao cho A(x) = B(x) + C(x).
Xem đáp án »
13/07/2024
4,235
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 01
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 01
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ nghịch (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận