Quan sát hình chữ nhật MNPQ ở Hình 3.

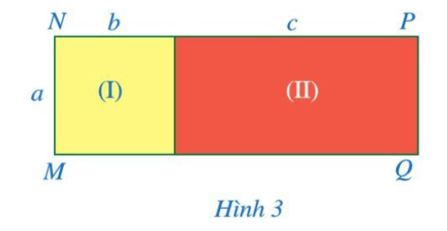
a) Tính diện tích mỗi hình chữ nhật (I), (II);

b) Tính diện tích của hình chữ nhật MNPQ;

c) So sánh: a(b + c) và ab + ac.

a) P(x) = (-2x² - 3x + x - 1)(3x² - x - 2).

= (-2x² - 2x - 1)(3x² - x - 2).

= -2x² . 3x² - (-2x²) . x - (-2x²) . 2 - 2x . 3x² - 2x . (-x) - 2x . (-2) - 1 . 3x² - 1 . (-x) - 1 . (-2)

= -6x⁴ + 2x³ + 4x² - 6x³ + 2x² + 4x - 3x² + x + 2

= -6x⁴ + (2x³ - 6x³) + (4x² + 2x² - 3x²) + (4x + x) + 2

= -6x⁴ - 4x³ + 3x² + 5x + 2

Khi đó đa thức P(x) có bậc bằng 4, hệ số cao nhất bằng -6, hệ số tự do bằng 2.

b) Q(x) = (x⁵ - 5)(-2x⁶ - x³ + 3)

= x⁵ . (-2x⁶) - x⁵ . x³ + x⁵ . 3 - 5 . (-2x⁶) - 5 . (-x³) - 5 . 3

= -2x¹¹ - x⁸ + 3x⁵ + 10x⁶ + 5x³ - 15

= -2x¹¹ - x⁸ + 10x⁶ + 3x⁵ + 5x³ - 15

Khi đó đa thức Q(x) có bậc bằng 11, hệ số cao nhất bằng -2, hệ số tự do bằng -15.

a) $\frac{1}{2}$x² . $\frac{6}{5}$x³ = $\frac{1}{2}$ . $\frac{6}{5}$ . x² . x³ = $\frac{3}{5}$x⁵.

b) y^{2$\left(\frac{5}{7}{y}^3-2y^2+\mathrm{0,25}\right)$} = y² . $\frac{5}{7}$y³ - y² . 2y² + y² . 0,25

= $\frac{5}{7}$y⁵ - 2y⁴ + 0,25y².

c) (2x² + x + 4)(x² - x - 1)

= 2x² . x² - 2x² . x - 2x² . 1 + x . x² - x . x - x . 1 + 4 . x² - 4 . x - 4 . 1

= 2x⁴ - 2x³ - 2x² + x³ - x² - x + 4x² - 4x - 4

= 2x⁴ + (-2x³ + x³) + (-2x² - x²+ 4x²) + (-x - 4x) - 4

= 2x⁴ - x³ + x² - 5x - 4.

d) (3x - 4)(2x + 1) - (x - 2)(6x + 3)

= 3x . 2x + 3x . 1 - 4 . 2x - 4 . 1 - (x . 6x + x . 3 - 2 . 6x - 2 . 3)

= 6x² + 3x - 8x - 4 - (6x² + 3x - 12x - 6)

= 6x² - 5x - 4 - (6x² - 9x - 6)

= 6x² - 5x - 4 - 6x² + 9x + 6

= (6x² - 6x²) + (-5x + 9x) + (-4 + 6)

= 4x + 2.