Biểu đồ đoạn thẳng ở Hình 3 biểu diễn tốc độ tăng trưởng GDP của Việt Nam giai đoạn 2012 – 2019. 

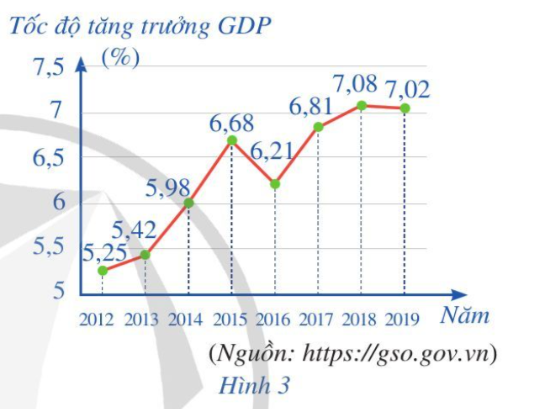
Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở Hình 3.

Hướng dẫn giải:

Số trung bình cộng của mẫu số liệu (5) là:

\[\overline {{x_{\left( 5 \right)}}} = \frac{{55,2 + 58,8 + 62,4 + 54 + 59,4}}{5} = 57,96\].

Phương sai của mẫu số liệu (5) là:

\(s_{\left( 5 \right)}^2 = \frac{{{{\left( {55,2 - 57,96} \right)}^2} + {{\left( {58,8 - 57,96} \right)}^2} + {{\left( {62,4 - 57,96} \right)}^2} + {{\left( {54 - 57,96} \right)}^2} + {{\left( {59,4 - 57,96} \right)}^2}}}{5}\)

= 9,1584.

Số trung bình cộng của mẫu số liệu (6) là:

\(\overline {{x_{\left( 6 \right)}}} = \frac{{271,2\; + 261\; + 276\; + 282\; + 270}}{5} = 272,04\).

Phương sai của mẫu số liệu (6) là:

\(s_{\left( 6 \right)}^2 = \frac{1}{5}\)[(271,2 − 272,04)² + (261 − 272,04)² + (276 − 272,04)² + (282 − 272,04)² + (270 − 272,04)²] = 48,3264.

Vì 9,1584 < 48,3264 nên \(s_{\left( 5 \right)}^2 < s_{\left( 6 \right)}^2\).

Vậy cự li chạy 500 m có kết quả đồng đều hơn.