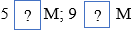Giải SGK Toán lớp 6 Bài 1: Tập hợp có đáp án - Kết nối tri thức
26 người thi tuần này 4.6 2.4 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Ôn tập chương IX (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 43. Xác suất thực nghiệm (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 42. Kết quả có thể và sự kiện trong trò chơi, thí nghiệm (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 41. Biểu đồ cột kép (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 40. Biểu đồ cột (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 39. Bảng thống kê và biểu đồ tranh (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 38: Dữ liệu và thu thập dữ liệu (Đúng sai - Trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Ôn tập chương 9 (Đúng sai - Trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
Giả sử trong lớp em có 4 tổ trưởng có tên là: Mai, Linh, Trang, Nhung
Khi đó: Tập hợp B gồm các bạn: Mai, Linh, Trang, Nhung
+) Bạn Linh thuộc tập hợp B.
+) Bạn Dũng không thuộc tập hợp B.
Lời giải
Bạn Nam viết sai vì theo cách mô tả của tập hợp thì mỗi phần tử chỉ được viết một lần nhưng ở đây chữ cái A, N xuất hiện hai lần.
Cách viết đúng là: L = {N; H; A; T; R; G}.
Lời giải
Chú ý: kí hiệu ℕ là tập hợp các số tự nhiên và ℕ* là tập hợp các số tự nhiên khác 0.
+) Ta có: A = { x ∈ ℕ | x < 5 }
Trong tập hợp A, ta thấy x ∈ ℕ và x < 5 nên x là các số tự nhiên nhỏ hơn 5, đó là: 0; 1; 2; 3; 4.
Do đó ta viết: A = {0; 1; 2; 3; 4}.
+) Ta có: B = {x ∈ ℕ* | x < 5}
Trong tập hợp B, ta thấy x ∈ ℕ* và x < 5 nên x là các số tự nhiên khác 0 và nhỏ hơn 5, đó là: 1; 2; 3; 4
Do đó ta viết: B = {1; 2; 3; 4}.
Lời giải
a) Nhận thấy các số tự nhiên lớn hơn 6 và nhỏ hơn 10 là các số: 7; 8; 9
Nên tập hợp M gồm các số: 7, 8, 9
Do đó: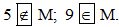
b) Do đó ta có mô tả tập hợp M theo hai cách như sau:
Cách 1: Liệt kê các phần tử của tập hợp
M = {7; 8; 9}.
Cách 2: Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
M = {x ∈ ℕ | 6 < x < 10}
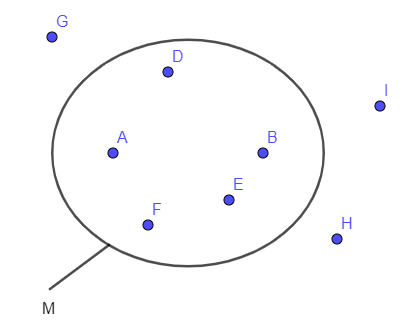
Lời giải
+) Tập hợp A có chứa phần tử a, hay a thuộc tập A và ta viết a ∈ A
Tập hợp B không chứa phần tử a, hay a không thuộc tập B và ta viết a ∉ B
+) Tập hợp A có chứa phần tử b, hay b thuộc tập A và ta viết b ∈ A
Tập hợp B có chứa phần tử b, hay b thuộc tập B và ta viết b ∈ B
+) Tập hợp A có chứa phần tử x, hay x thuộc tập A và ta viết x ∈ A
Tập hợp B không chứa phần tử x, hay x không thuộc tập B và ta viết x ∉ B
+) Tập hợp A không chứa phần tử u, hay u không thuộc tập A và ta viết u ∉ A
Tập hợp B có chứa phần tử u, hay u thuộc tập B và ta viết u ∈ B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.