Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m,
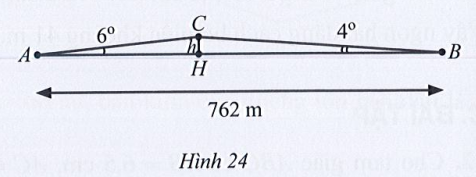
Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m,
Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Đặt AH = x (m) (x > 0)
⇒ BH = AB – AH = 762 – x (m)
Xét tam giác AHC vuông tại H, có:
\(\tan A = \frac{{CH}}{{AH}}\)
⇔ \(\tan 6^\circ = \frac{{CH}}{x}\)
⇔ CH = tan6°.x
Xét tam giác BHC vuông tại H, có:
\(\tan B = \frac{{CH}}{{BH}}\)
⇔ \(\tan 4^\circ = \frac{{CH}}{{762 - x}}\)
⇔ CH = tan4°.(762 – x)
⇒ tan6°.x = tan4°.(762 – x)
⇔ (tan6° + tan4°).x ≈ 53,3
⇔ x ≈ 304,4
⇒ CH ≈ tan6°.304,4 ≈ 32
Vậy chiều cao của con dốc là 32 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
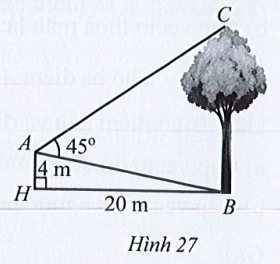
Xét tám giác vuông AHB, có:
AB2 = AH2 + HB2 (định lí pythagoras)
⇔ AB2 = 42 + 202
⇔ AB2 = 416
⇔ AB ≈ 20,4
Ta lại có: \(\tan \widehat {HAB} = \frac{{HB}}{{HA}}\) ⇔ \(\tan \widehat {HAB} = \frac{{20}}{4} = 5 \Rightarrow \widehat {HAB} \approx 78,7^\circ \)
Ta có: AH ⊥ BH và CB ⊥ BH nên AH // CB
⇒ \(\widehat {HAB} = \widehat {ABC} \approx 78,7^\circ \) (hai góc so le trong)
Xét tam giác ABC có:
\(\widehat C = 180^\circ - \widehat {BAC} - \widehat {ABC} = 180^\circ - 45^\circ - 78,7^\circ \)= 56,3°.
Áp dụng định lí sin trong tam giác ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
⇔ \(BC = \frac{{AB\sin A}}{{\sin C}} = \frac{{20,4.\sin 45^\circ }}{{\sin 56,3^\circ }} \approx 17,3\).
Vậy chiều cao của cây là 17,3 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
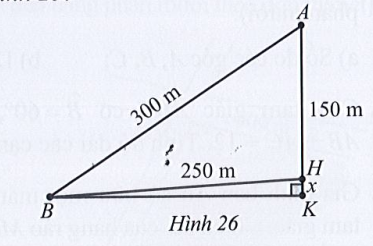
Xét tam giác ABC, có:
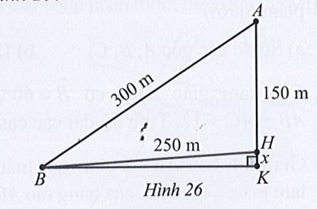
\[{\rm{cos}}\widehat {AHB} = \frac{{A{H^2} + B{H^2} - A{B^2}}}{{2.AH.BH}} = \frac{{{{150}^2} + {{250}^2} - {{300}^2}}}{{2.150.250}} = - \frac{1}{{15}}\]
⇒ \[\widehat {AHB} \approx 93,8^\circ \]
Ta lại có: \(\widehat {AHB} + \widehat {BHK} = 180^\circ \)
\(\widehat {BHK} = 180^\circ - \widehat {AHB} = 180^\circ - 93,8^\circ = 86,2^\circ \)
Xét tam giác BHK vuông tại K, có:
\(\widehat {HBK} + \widehat {BHK} = 90^\circ \) (hai góc phụ nhau)
⇔ \(\widehat {HBK} = 90^\circ - \widehat {BHK}\)
⇔ \(\widehat {HBK} \approx 90^\circ - 86,2^\circ = 3,8^\circ \).
Vậy độ dốc của cầu qua trụ khoảng 3,8°.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập