Giải SBT Toán 10 CD Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án

Lời giải

Xét tam giác ABC, có:

BC² = AB² + AC² – 2.AB.AC.cosA

⇔ BC² = 6,5² + 8,5² – 2.6,5.8,5.cos125°

⇔ BC² ≈ 177,9

⇔ BC ≈ 13,3.

 Vậy BC ≈ 13,3.

Xét tam giác ABC, có:

\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{{{6,5}^2} + {{13,3}^2} - {{8,5}^2}}}{{2.6,5.13,3}} \approx 0,8\)

⇒ \(\widehat B \approx 31,8^\circ \)

Ta lại có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)

⇒ \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) \approx 180^\circ - \left( {125^\circ + 31,8^\circ } \right) = 23,2^\circ \).

Vậy \(\widehat B \approx 31,8^\circ \) và \(\widehat C \approx 23,2^\circ \).

Lời giải

Lời giải

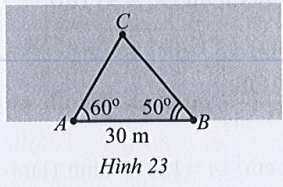
Xét tam giác ABC, có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)

⇒ \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) = 180^\circ - \left( {65^\circ + 45^\circ } \right) = 70^\circ \).

Áp dụng định lí sin trong tam giác ABC, ta được:

\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)

⇔ \(\frac{{AB}}{{\sin 45^\circ }} = \frac{{AC}}{{\sin 65^\circ }} = \frac{{50}}{{\sin 70^\circ }} = 2R\)

⇒ \(\frac{{AB}}{{\sin 45^\circ }} = \frac{{50}}{{\sin 70^\circ }}\) ⇔ \(AB = \frac{{50.\sin 45^\circ }}{{\sin 70^\circ }} \approx 37,6\)

⇒ \(\frac{{AC}}{{\sin 65^\circ }} = \frac{{50}}{{\sin 70^\circ }}\) ⇔ \(AC = \frac{{50\sin 65^\circ }}{{\sin 70^\circ }} \approx 48,2\)

Vậy AB ≈ 37,6 vậy AC ≈ 48,2.

Lời giải

Lời giải

Xét tam giác ABC, có:

Áp đụng hệ quả của định lí cos ta được:

\(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{5^2} + {8^2} - {9^2}}}{{2.5.8}} = \frac{1}{{10}} \Rightarrow \widehat A \approx 84,3^\circ ;\)

\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{{5^2} + {9^2} - {8^2}}}{{2.5.9}} = \frac{7}{{15}} \Rightarrow \widehat B \approx 62,2^\circ ;\)

\(\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.BC.AC}} = \frac{{{8^2} + {9^2} - {5^2}}}{{2.8.9}} = \frac{5}{6} \Rightarrow \widehat C \approx 33,5^\circ ;\)

Vậy \(\widehat A \approx 84,3^\circ ,\widehat B \approx 62,2^\circ ,\widehat C \approx 33,5^\circ \).