Quan sát cây cầu văng minh họa ở Hình 25.
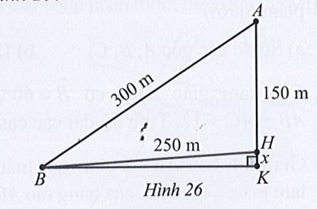
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
Quan sát cây cầu văng minh họa ở Hình 25.


Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
Quảng cáo
Trả lời:
Lời giải
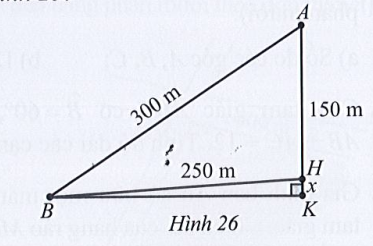
Xét tam giác ABC, có:
\[{\rm{cos}}\widehat {AHB} = \frac{{A{H^2} + B{H^2} - A{B^2}}}{{2.AH.BH}} = \frac{{{{150}^2} + {{250}^2} - {{300}^2}}}{{2.150.250}} = - \frac{1}{{15}}\]
⇒ \[\widehat {AHB} \approx 93,8^\circ \]
Ta lại có: \(\widehat {AHB} + \widehat {BHK} = 180^\circ \)
\(\widehat {BHK} = 180^\circ - \widehat {AHB} = 180^\circ - 93,8^\circ = 86,2^\circ \)
Xét tam giác BHK vuông tại K, có:
\(\widehat {HBK} + \widehat {BHK} = 90^\circ \) (hai góc phụ nhau)
⇔ \(\widehat {HBK} = 90^\circ - \widehat {BHK}\)
⇔ \(\widehat {HBK} \approx 90^\circ - 86,2^\circ = 3,8^\circ \).
Vậy độ dốc của cầu qua trụ khoảng 3,8°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
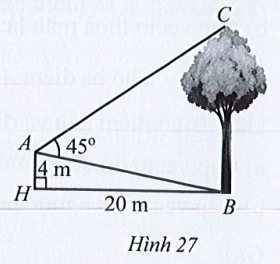
Xét tám giác vuông AHB, có:
AB2 = AH2 + HB2 (định lí pythagoras)
⇔ AB2 = 42 + 202
⇔ AB2 = 416
⇔ AB ≈ 20,4
Ta lại có: \(\tan \widehat {HAB} = \frac{{HB}}{{HA}}\) ⇔ \(\tan \widehat {HAB} = \frac{{20}}{4} = 5 \Rightarrow \widehat {HAB} \approx 78,7^\circ \)
Ta có: AH ⊥ BH và CB ⊥ BH nên AH // CB
⇒ \(\widehat {HAB} = \widehat {ABC} \approx 78,7^\circ \) (hai góc so le trong)
Xét tam giác ABC có:
\(\widehat C = 180^\circ - \widehat {BAC} - \widehat {ABC} = 180^\circ - 45^\circ - 78,7^\circ \)= 56,3°.
Áp dụng định lí sin trong tam giác ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
⇔ \(BC = \frac{{AB\sin A}}{{\sin C}} = \frac{{20,4.\sin 45^\circ }}{{\sin 56,3^\circ }} \approx 17,3\).
Vậy chiều cao của cây là 17,3 m.
Lời giải
Lời giải
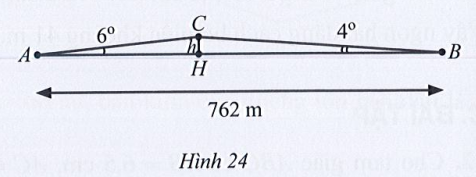
Xét tam giác ABC, có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)
⇒ \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) = 180^\circ - \left( {65^\circ + 45^\circ } \right) = 70^\circ \).
Áp dụng định lí sin trong tam giác ABC, ta được:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
⇔ \(\frac{{AB}}{{\sin 45^\circ }} = \frac{{AC}}{{\sin 65^\circ }} = \frac{{50}}{{\sin 70^\circ }} = 2R\)
⇒ \(\frac{{AB}}{{\sin 45^\circ }} = \frac{{50}}{{\sin 70^\circ }}\) ⇔ \(AB = \frac{{50.\sin 45^\circ }}{{\sin 70^\circ }} \approx 37,6\)
⇒ \(\frac{{AC}}{{\sin 65^\circ }} = \frac{{50}}{{\sin 70^\circ }}\) ⇔ \(AC = \frac{{50\sin 65^\circ }}{{\sin 70^\circ }} \approx 48,2\)
Vậy AB ≈ 37,6 vậy AC ≈ 48,2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.