Cho tứ giác ABCD, O là trung điểm của AB. Chứng minh: \(\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AC} + \overrightarrow {BD} .\)

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 10 CD Bài 4. Tổng và hiệu của hai vectơ có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

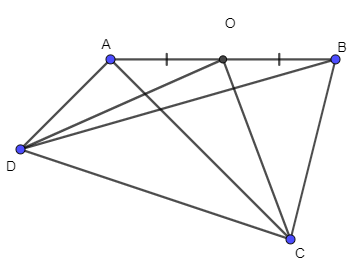
Media VietJack

Ta có: \(\overrightarrow {AC} + \overrightarrow {BD} \)

\( = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {BO} + \overrightarrow {OD} } \right)\)

\( = \left( {\overrightarrow {AO} + \overrightarrow {BO} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right)\)

\( = \overrightarrow 0 + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right)\)

\( = \overrightarrow {OC} + \overrightarrow {OD} \).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng?

A. \(\overrightarrow {MN} - \overrightarrow {NP} = \overrightarrow {MP} \).

B. \( - \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \).

C. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \).

D. \(\overrightarrow {MN} + \overrightarrow {NP} = - \overrightarrow {MP} \).

Xem đáp án

Lời giải

Đáp án đúng là C

Ta có: \(\overrightarrow {MN} - \overrightarrow {NP} = \overrightarrow {MN} + \overrightarrow {PN} = \overrightarrow {MN} + \overrightarrow {MK} = \overrightarrow {MH} \ne \overrightarrow {MP} \) (H, K là điểm thỏa mãn MKHN là hình bình hành). Do đó A sai.

Ta có: \( - \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow {NT} \ne \overrightarrow {MP} \)(T là điểm MNPT là hình bình hành). Do đó B sai

Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \) (quy tắc ba điểm). Do đó C đúng.

Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \ne - \overrightarrow {MP} \). Do đó D sai.

Câu 2

Cho tam giác ABC. Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là:

A. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} \).

B. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \).

C. \(\overrightarrow {GC} + \overrightarrow {GB} = \overrightarrow {GA} \).

D. \(\overrightarrow {GA} + \overrightarrow {GB} - \overrightarrow {GC} = \overrightarrow 0 \).

Xem đáp án

Lời giải

Đáp án đúng là B

Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

⇔ \(\overrightarrow {GB} + \overrightarrow {GC} = - \overrightarrow {GA} \)

⇔ \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \)

Câu 3