Câu hỏi trong đề: Giải VTH Toán 7 Luyện tập chung trang 68 có đáp án !!
Quảng cáo
Trả lời:
|
GT |
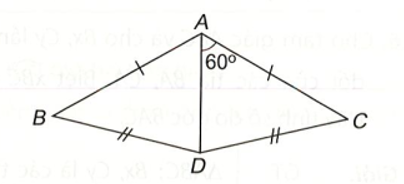
∆ABC, , M ∈ BC, |
|
KL |
Tính . |
Vì AMB và AMC là hai góc kề bù nên ta có:
⇒
Do tổng ba góc trong tam giác ABM bằng 180° nên ta có:
.
Vì M nằm trên cạnh BC nên .
Do tổng ba góc trong tam giác ABC bằng 180° nên ta có:
Kết luận:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
GT |
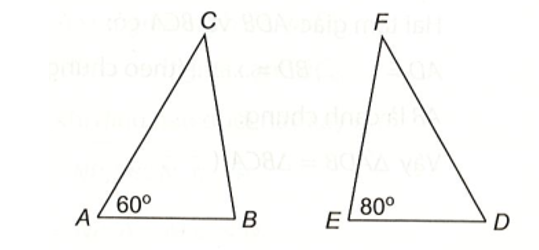
∆ABC = ∆DEF, |
|
KL |
Tính . |
Vì ∆ABC = ∆DEF nên ta suy ra:
và (các cặp góc tương ứng bằng nhau)
Do tổng ba góc trong tam giác DEF bằng 180° nên ta có:
Kết luận
Lời giải
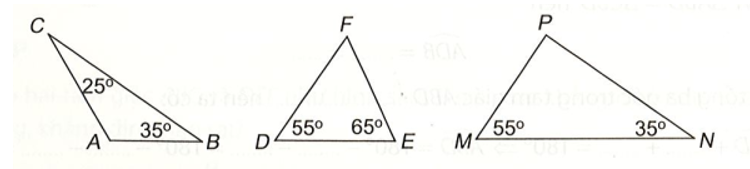
Vì tổng ba góc trong tam giác ABC bằng 180° nên ta có:
⇒
Tương tự trong tam giác DEF ta có
⇒
Cuối cùng trong tam giác MNP ta có
⇒
Kết luận: và chỉ có tam giác MNP có một góc vuông nên chỉ có MNP là tam giác vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.