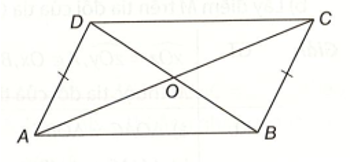
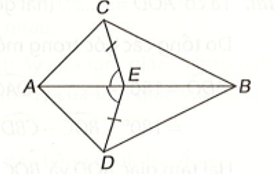
Cho hình vẽ dưới dây. Biết rằng AD = BC, DAC^=CBD^, O là giao điểm của AC và BD. Chứng minh rằng AO = BO.

Ta có: AOD^=BOC^ (hai góc đối đỉnh) Do tổng các góc trong mỗi tam giác ADO và BCO bằng 180° nên ta có: ADO^=180°−AOD^−DAO^=180°−BOC^−CBO^=BCO^. Hai tam giác AOD và BOC có: ADO^=BCO^ (theo chứng minh trên) AD = BC (theo giả thiết) DAO^=DAC^=CBD^=CBO^(theo giả thiết). Vậy tam giác ∆AOD = ∆BOC (g – c – g).

Câu hỏi:

12/07/2024 1,246

Cho hình vẽ dưới dây. Biết rằng AD = BC, $\hat{D A C} = \hat{C B D}$ , O là giao điểm của AC và BD. Chứng minh rằng AO = BO.

Xem lời giải

Câu hỏi trong đề: Giải VTH Toán 7 Luyện tập chung trang 74 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

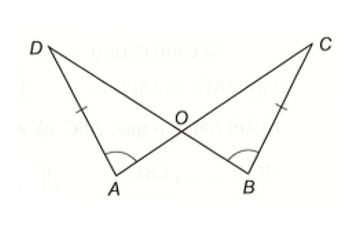
Cho hình vẽ dưới dây. Biết rằng AD = BC,góc DAC= góc CBD , O là giao điểm của AC (ảnh 1)

Ta có: $\hat{A O D} = \hat{B O C}$ (hai góc đối đỉnh)

Do tổng các góc trong mỗi tam giác ADO và BCO bằng 180° nên ta có:

$\hat{A D O} = 180 ° - \hat{A O D} - \hat{D A O} = 180 ° - \hat{B O C} - \hat{C B O} = \hat{B C O}$ .

Hai tam giác AOD và BOC có:

$\hat{A D O} = \hat{B C O}$ (theo chứng minh trên)

AD = BC (theo giả thiết)

$\hat{D A O} = \hat{D A C} = \hat{C B D} = \hat{C B O}$ (theo giả thiết).

Vậy tam giác ∆AOD = ∆BOC (g – c – g).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF, $\hat{B A C} = \hat{E D F} = 60 °,$ BC = 6 cm, $\hat{A B C} = 45 ° .$ Tính độ dài cạnh EF và số đo các góc C, E, F.

Xem đáp án

Lời giải

∆ABC và ∆DEF, AB = DE, AC = DF,

$\hat{B A C} = \hat{E D F} = 60 °,$ BC = 6 cm, $\hat{A B C} = 45 ° .$

Tính EF, $\hat{C}, \hat{E}, \hat{F}$ .

Từ giả thiết suy ra ∆ABC = ∆DEF (c – g – c) vì AB = DE, $\hat{A} = \hat{D} = 60 °,$ AC = DF (theo giả thiết). Do các cạnh tương ứng của hai tam giác bằng nhau là bằng nhau nên ta có:

EF = BC = 6cm, $\hat{E} = \hat{B} = 45 °$ , $\hat{F} = \hat{C}$

Do tổng ba góc trong tam giác ABC bằng 180° nên:

$\hat{C} = 180 ° - \hat{A} - \hat{B} = 180 ° - 60 ° - 45 ° = 75 °$ , suy ra $\hat{F} = \hat{C} = 75 °$ .

Kết luận EF = 6 cm, $\hat{C} = 75 °$ , $\hat{E} = 45 °$ , $\hat{F} = 75 °$

Câu 2

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\hat{C A O} = \hat{C B O} .$

a) Chứng minh rằng ∆OAC = ∆OBC.

Xem đáp án

Lời giải

$\hat{x O y} = \hat{y O z}$ , A ∈ Ox, B ∈ Oy, C ∈ Oz, $\hat{C A O} = \hat{C B O} .$ ,

M thuộc tia đối của tia CO

a) ∆OAC = ∆OBC.

b) ∆MAC = ∆MBC.

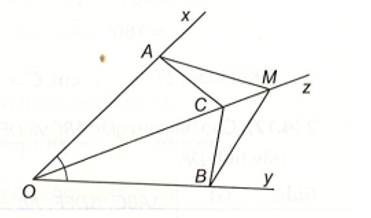
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các (ảnh 1)

a) Xét hai tam giác OAC và OBC, ta có:

$\hat{C O A} = \hat{C O B}$ (OC là tia phân giác của góc AOB);

OC là cạnh chung;

$\hat{A C O} = 180 ° - \hat{C A O} - \hat{C O A}$

$= 180 ° - \hat{C B O} - \hat{C O B} = \hat{B C O}$

Vậy ∆OAC = ∆OBC (g – c – g).

Câu 3

Cho hình vẽ đưới đây. Biết đường thẳng AD song song với đường thẳng BC, AD = BC. Chứng minh rằng AB song song với CD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng ∆MAC = ∆MBC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\hat{B} = \hat{E} = 70 °, \hat{A} = \hat{D} = 60 °,$ AC = 6 cm. Hãy tính DF.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho năm điểm A, B, C, D, E thỏa mãn EC = ED và $\hat{A E C} = \hat{A ED}$ như hình vẽ dưới đây. Chứng minh rằng:

a) ∆AEC = ∆AED;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho hình vẽ dưới dây. Biết rằng AD = BC, $\hat{D A C} = \hat{C B D}$ , O là giao điểm của AC và BD. Chứng minh rằng AO = BO.

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF, $\hat{B A C} = \hat{E D F} = 60 °,$ BC = 6 cm, $\hat{A B C} = 45 ° .$ Tính độ dài cạnh EF và số đo các góc C, E, F.

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\hat{C A O} = \hat{C B O} .$

a) Chứng minh rằng ∆OAC = ∆OBC.

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\hat{B} = \hat{E} = 70 °, \hat{A} = \hat{D} = 60 °,$ AC = 6 cm. Hãy tính DF.

Cho năm điểm A, B, C, D, E thỏa mãn EC = ED và $\hat{A E C} = \hat{A ED}$ như hình vẽ dưới đây. Chứng minh rằng:

a) ∆AEC = ∆AED;