Câu hỏi:

12/07/2024 366

b) Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho.

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề toán 9 Chuyên đề 5: Cung chứa góc có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

b) Phần thuận: Trong đường tròn đường kính AB ta có: (góc nội tiếp chắn nửa đường tròn).

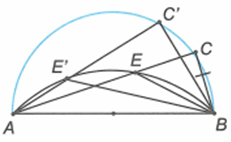
b) Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho. (ảnh 1)

Mà CE = CB (giả thiết) nên suy ra $Δ C B E$ vuông tại C.

$\Rightarrow \hat{C E B} = 45 ° \Rightarrow \hat{A E B} = 180 ° - \hat{C E B} = 135 °$ (hai góc kề bù).

Mặt khác, AB cố định, nên khi C chuyển động trên đường tròn đường kính AB thì E chuyển động trên cung chứa góc $135 °$ dựng trên đoạn thẳng AB cố định.

Giới hạn: Khi dây AC có độ dài lớn nhất bằng đường kính của đường tròn, thì C trùng với B khi đó E trùng với B. Suy ra B là một điểm của quỹ tích.

Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A, thì khi đó E trùng với A nên A là một điểm của quỹ tích.

Phần đảo: Lấy E' bất kỳ trên cung chứa góc $135 °$ . Kẻ AE' cắt đường tròn đường kính AB tại C'. Nối BE', BC'.

Ta có: $\hat{A E^{'} B} = 135 °$ (vì E nằm trên cung chứa góc $135 °$ ).

$\Rightarrow \hat{B E^{'} C^{'}} = 180 ° - \hat{A E^{'} B} = 45 °$ (hai góc kề bù).

Trong đường tròn đường kính AB có: $\hat{A C^{'} B} = 90 °$ (góc nội tiếp chắn nửa đường tròn).

Suy ra tam giác E'C'B vuông cân tại C'. Do đó C'E = C'B.

Vậy C' là một điểm thuộc quỹ tích.

Kết luận: Vậy E chuyển động trên một cung chứa góc

135 °

vẽ trên đoạn AB, nằm trên nửa mặt phẳng bờ AB chứa điểm C.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB (C khác A và B). Chứng minh rằng tâm I của đường tròn nội tiếp tam giác ABC chuyển động trên một cung tròn cố định.

Xem đáp án

Lời giải

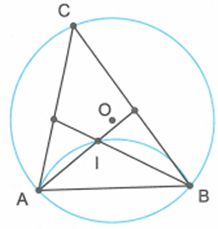
Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB ( C khác A và B ). (ảnh 1)

Vì dây AB cố định nên

\hat{A C B} = \frac{1}{2} s đ \overset{⏜}{A B}

không đổi.

Đặt $\hat{A C B} = α$ . Ta có:

$\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc trong một tam giác).

$\Rightarrow \hat{B A C} + \hat{A B C} = 180 ° - \hat{A C B} = 180 ° - α$ .

Vì I là tâm đường tròn nội tiếp tam giác ABC nên AI, BI lần lượt là tia phân giác của hai góc A và B. Suy ra

$\hat{I A B} = \frac{1}{2} \hat{B A C}; \hat{I B A} = \frac{1}{2} \hat{A B C} \Rightarrow \hat{I A B} + \hat{I B A} = \frac{1}{2} (\hat{B A C} + \hat{A B C}) = 90 ° - \frac{α}{2}$

Lại có: $\hat{A I B} + \hat{I A B} + \hat{I B A} = 180 °$ (tổng ba góc trong một tam giác).

$\Rightarrow \hat{A I B} = 180 ° - (\hat{I A B} + \hat{I B A}) = 180 ° - (90 ° - \frac{α}{2}) = 90 ° + \frac{α}{2}$ không đổi.

Vì AB cố định, I thuộc nửa mặt phẳng chứa cung lớn AB có bờ là đường thẳng AB nên I luôn chuyển động trên cung chứa góc $90 ° + \frac{α}{2}$ dựng trên đoạn AB.

Câu 2

Cho nửa đường tròn (O;R) đường kính AB. Vẽ dây MN = R (điểm M ở trên cung $\overset{⏜}{A N}$ ). Hai dây AN và BM cắt nhau tại I. Hỏi khi dây MN di động thì điểm I di động trên đường nào?

Xem đáp án

Lời giải

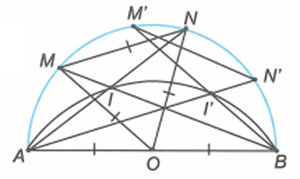
Cho nửa đường tròn (O; R) đường kính AB . Vẽ dây MN = R (điểm M ở trên cung AN ). (ảnh 1)

Phần thuận: Tam giác MON đều (vì

O M = O N = M N = R

\Rightarrow \hat{M O N} = 60 ° \Rightarrow s đ \overset{⏜}{M N} = 60 ° \Rightarrow s đ \overset{⏜}{A M} + s đ \overset{⏜}{N B} = 180 ° - 60 ° = 120 ° \Rightarrow \hat{N I B} = \frac{1}{2} (s đ \overset{⏜}{A M} + s đ \overset{⏜}{N B}) = 60 °

Ta có: $\hat{A I B} = 180 ° - \hat{N I B} = 120 °$ (hai góc kề bù).

Do AB cố định nên quỹ tích điểm I là cung chứa góc $120 °$ dựng trên đoạn AB.

Phần đảo: Trên cung chứa góc $120 °$ dựng trên đoạn AB, lấy điểm I'. AI' và BI' lần lượt cắt nửa đường tròn (O) tại N' và M'. Khi đó $\hat{A I^{'} B} = 120 ° \Rightarrow \hat{B I^{'} N^{'}} = 60 ° \Rightarrow \hat{M^{'} O N^{'}} = 60 °$ .

Suy ra tam giác M'O'N' đều. Do đó M'N' = R.

Vậy I' là một điểm thuộc quỹ tích.

Kết luận: Quỹ tích các điểm I là cung chứa góc $120^{\circ}$ dựng trên đoạn AB.

Câu 3